55.跳跃游戏.md

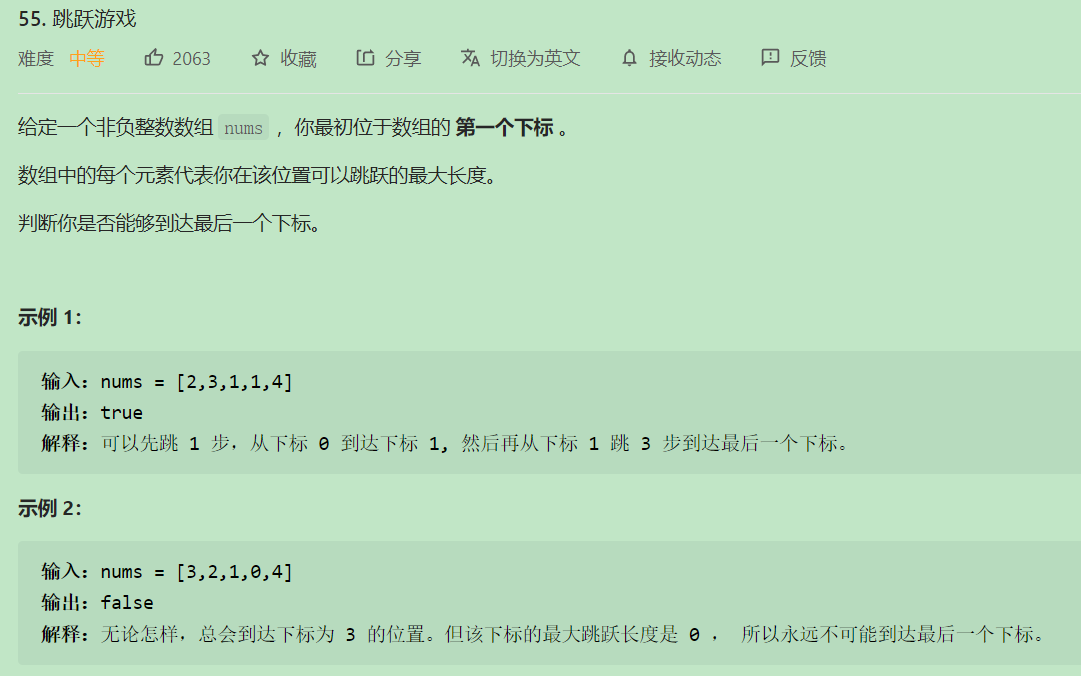
// 贪心算法。在我看来，贪心算法一直是相对难以思考的问题，有点类似脑筋急转弯。“从局部最优到全局最优”是关键。
// 根据题干，可以初步判断此题要么是考察数组，要么是考察一种巧妙的思想，读懂并理解题意并找到巧妙的点，是解题
// 的关键。

// 初步读题，可以判断是需要for遍历数组的，且问题的最后一句，判断是否能达到最后一个下标，容易引人想到采用dp
// 的方法，vector<bool> dp(n, 0)，每个dp[i]代表位置是否能到达。到这一切合理，但递推公式会出问题。思考dp的
// 递推，dp[i]来自于什么？可以来自dp[i-1]、可以来自dp[i-2]、...甚至可来自dp[0]，这就尴尬了，初步说明dp是
// 行不通的。

// 之前提到，这种题读题没有明显思路，且需要找到巧妙的点，此时就要考虑到贪心算法了，因为这就是贪心算法的特征。
// 再次读题，可以发现遍历数组for()，“是否能到达最后一个下标”等，都其实也是贪心算法的特征。

// 乍一看唬人，根据贪心算法来遍历数组for()，对每个i进行处理，考虑需要处理什么？“结合局部最优到全局最优”，
// 就可以想到此题的关键，即处理i：计算当前位置i，能走到的最远距离。遍历过程中，对每个i计算该距离，直到遍历结束
// 如果在此期间，某个i的该最远距离超过(>=)了size-1，那么就true，否则就false。
// 思路有了，进行实现。上述的for()过程每个位置i，都要有记录个最远距离，所以考虑维护一个dp[n]数组，装每个i对应
// 的最远距离。最远距离用索引坐标表示。

// 示例1：nums = [2,3,1,1,4]。dp[0]=2 dp[1]=4 因为dp[1]>=size-1，返回true。
// 示例2: nums = [3,2,1,0,4]。dp[0]=3 dp[1]=3 dp[2]=3 dp[3]=3 此时有个前提，那就是遍历过程的i，得<=之前
// 距离的最大值，否则如果都走不到i那去，还就可以直接返回false了，路断了属于是。所以在此还需加上一个max_idx
// 用于更新每次遍历的最大值。

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n = nums.size();
        // 维护一个dp[n]数组，装for()循环中，每个i对应的最远距离，看是否哪个i能超过终点。
        vector<int> dp(n, 0);
        // 遍历i有个前提，那就是i得<=之前距离的最大值，否则如果都走不到i那去，
        // 还就可以直接返回false了，路断了属于是。比如示例2当i=4时。
        int max_idx = 0;
        for (int i = 0; i < n; i++) {
            // 对i的遍历限制，如果之前持续更新的最远距离max_idx都不能达到i，那直接路断，返回false。
            if (i <= max_idx) {
                // 本题关键，更新dp[i]，当前i能辐射的最远距离。
                dp[i] = i + nums[i];
                // 紧接着，更新max_idx，用于限制遍历i，判断是否路断。
                max_idx = max(max_idx, dp[i]);
                // 一旦遍历i过程中，哪个i突破了终点，那么返回true。
                if (dp[i] >= n - 1) {
                    return true;
                }
            } else {
                return false;
            }
        }
        // 这里必须要一个返回值，但应该无论如何，都走不到这里，前面的两个return会包含所有情况。
        // 对于[3 2 1 0 4]，会在遍历i=4时，判断路断，return false；
        // 对于[2 2 1 1 0]，会在遍历i=4时，dp[4]=4+0=4>=n-1=4，return true。
        // 因此无论如何，都走不到最外面来。
        return true;
    }
};

// 基础用例
// 输入：nums = [3,2,1,0,4]
// 输出：false

// 特殊用例
// 输入：[2,0,0]
// 输出：true

// 核心思想：维护max_len = max(max_len, i + nums[i]);看i是否能跨越max_len。

class Solution {
public:
    bool canJump(vector<int>& nums) {
        if (nums.size() <= 1) return true;
        int max_len = INT_MIN;
        int i = 0;
        for (; i < nums.size(); i++) {
            max_len = max(max_len, i + nums[i]);
            if (max_len >= nums.size() - 1) return true;
            if (i >= max_len) {
                // cout<<"break: "<<i<<" "<<max_len<<" "<<endl;
                break;
            }
            // cout<<i<<" "<<endl;
        }
    
        if (i == nums.size()) {
            return true;
        } else {
            return false;
        }
    }
};