221.最大正方形.md

// 复习

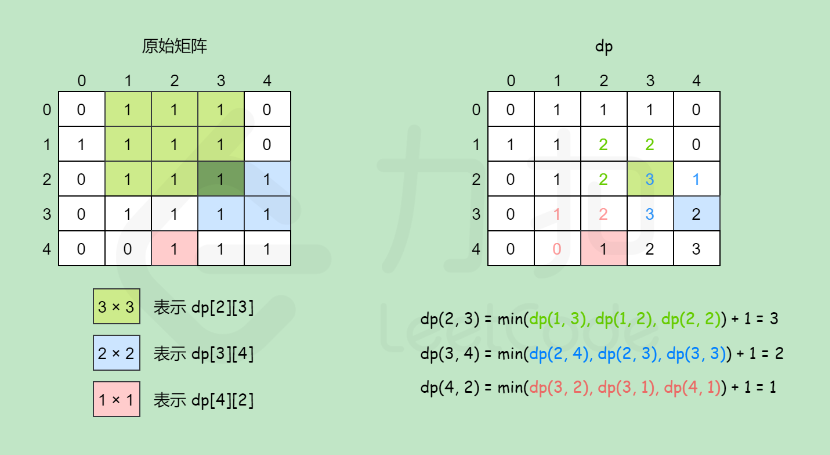
// 原始矩阵：
0 1 1 1 0
1 1 1 1 0
0 1 1 1 1
0 1 1 1 1
0 0 1 1 1

// dp矩阵
0 1 1 1 0
1 1 2 2 0
0 1 2 3 1
0 1 2 3 2
0 0 1 2 3

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.size() == 0)
            return 0;

        // dp[i][j]含义。
        // 注意二维dp[i][j]定义时的写法，稍不注意会忘。
        // dp[i][j]的含义，是此题的难点。含义为：对于i、j位置，dp[i][j]为以i、j作为右下角顶点时，能形成的最大正方形边长。
        // 可见，此题dp[i][j]有2重诡异。1）不是全局最大正方形；2）不是题干最大正方形面积，而是边长。
        vector<vector<int>> dp(matrix.size(), vector<int>(matrix[0].size(), 0));

        int max_val = INT_MIN;

        for (int i = 0; i < matrix.size(); i++) {
            for (int j = 0; j < matrix[0].size(); j++) {
                // 容易出错和很难找出bug的点，这里是'1'，char类型的网格。
                if (matrix[i][j] == '1') {
                    // dp[i][j]初始化。
                    // dp[i][j]网格的初始化，往往还是第一行和第一列，但此题的特殊之处在于，是一边进行for循环，一边进行
                    // 初始化，而不是一开始在for循环遍历之前就初始化完成。
                    // 正因如此，此题对于第一行dp[0][j]和第一列dp[i][0]，并不都初始化，只在满足m[i][j]=1的条件时才初始
                    // 化，不满足时则该dp[i][j]位置默认为0。这是因为只有第一行第一列遇到m[i][j]=1，该dp[i][j]才为1，
                    // 此处要仔细理解dp[i][j]的含义，只有理解了才有可能想到这一点。
                    if (i == 0 || j == 0) {
                        dp[i][j] = 1;
                    } else {
                        // dp[i][j]递推公式。
                        // 这也是此题难点，居然有这么一个说法，测试证明是正确的。
                        // dp[i][j]为左、上、左上3个的最小值+1。推导暂不明白，记住吧。
                        dp[i][j] = min(min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
                    }
                }
                // 用于记录整个for遍历，dp[i][j]的最大值。
                max_val = max(dp[i][j], max_val);
            }
        }

        // 返回最大面积。
        return max_val * max_val;
    }
};