215.数组中的第k个最大元素.md

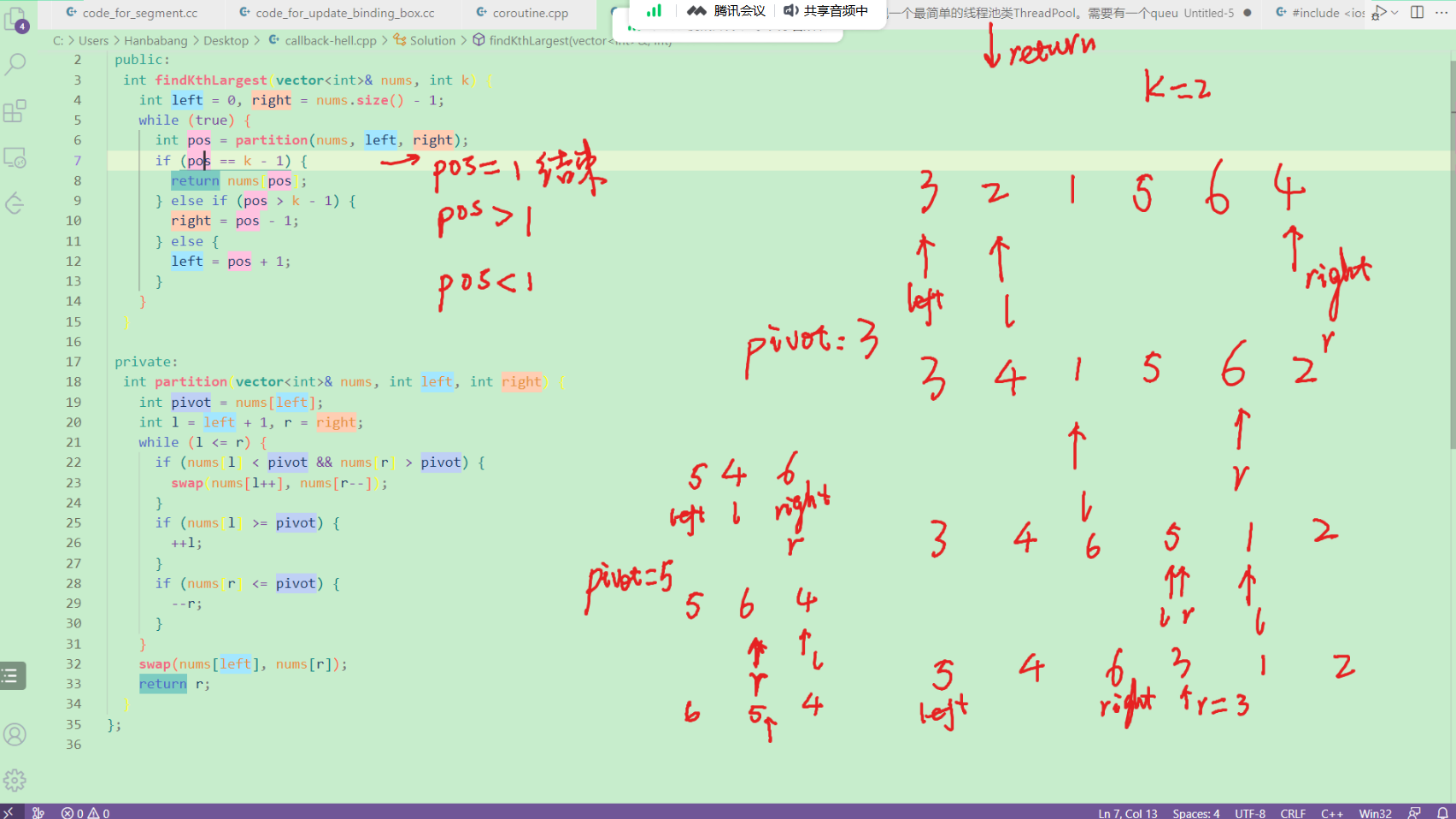
分支算法/快速排序
nums=3 2 1 5 6 4 k=2
利用快速排序的思想，定pivot(nums[left]=3)，通过left/right和pivot对比，
第一轮partition将大于3的放在左边，将小于3的放在右边（倒序），此过程中l++/r--，
然后将pivot放在left和right相交处，返回pos为3。
    
pos的正确答案为1（表示答案为nums[1]，即第2大的元素索引为1，左边只有一个比其大的数）。
我们的目标就是找到正确的pos。

因此，第一轮partition结束后，发现pos=3在目标索引pos=1的右边，说明目前的pos为第4大的数。
此时数组为5 4 6 3(pos=3) 1 2。因此此时将pos左边的5 4 6 3继续做partition，即right=pos-1。
反复此过程，最终第二轮partition得到6 5(pos=1) 4，此时pos=1为目标索引，所以找到答案。

class Solution {
 public:
  int findKthLargest(vector<int>& nums, int k) {
    int left = 0, right = nums.size() - 1;
    while (true) {
      int pos = partition(nums, left, right);
      if (pos == k - 1) {
        return nums[pos];
      } else if (pos > k - 1) {
        right = pos - 1;
      } else {
        left = pos + 1;
      }
    }
  }

 private:
  int partition(vector<int>& nums, int left, int right) {
    int pivot = nums[left];
    int l = left + 1, r = right;
    while (l <= r) {
      if (nums[l] < pivot && nums[r] > pivot) {
        swap(nums[l++], nums[r--]);
      }
      if (nums[l] >= pivot) {
        ++l;
      }
      if (nums[r] <= pivot) {
        --r;
      }
    }
    swap(nums[left], nums[r]);
    return r;
  }
};