参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
本题力扣上没有原题,大家可以去卡码网第46题去练习
《代码随想录》算法视频公开课:带你学透0-1背包问题!(滚动数组),相信结合视频再看本篇题解,更有助于大家对本题的理解。
昨天动态规划:关于01背包问题,你该了解这些!中是用二维dp数组来讲解01背包。
今天我们就来说一说滚动数组,其实在前面的题目中我们已经用到过滚动数组了,就是把二维dp降为一维dp,一些录友当时还表示比较困惑。
那么我们通过01背包,来彻底讲一讲滚动数组!
接下来还是用如下这个例子来进行讲解
背包最大重量为4。
物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?
对于背包问题其实状态都是可以压缩的。
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了,只用dp[j](一维数组,也可以理解是一个滚动数组)。
这就是滚动数组的由来,需要满足的条件是上一层可以重复利用,直接拷贝到当前层。
读到这里估计大家都忘了 dp[i][j]里的i和j表达的是什么了,i是物品,j是背包容量。
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
一定要时刻记住这里i和j的含义,要不然很容易看懵了。
动规五部曲分析如下:
- 确定dp数组的定义
关于dp数组的定义,我在 01背包理论基础 有详细讲解
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
- 一维dp数组的递推公式
二维dp数组的递推公式为: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
公式是怎么来的 在这里 01背包理论基础 有详细讲解。
一维dp数组,其实就上上一层 dp[i-1] 这一层 拷贝的 dp[i]来。
所以在 上面递推公式的基础上,去掉i这个维度就好。
递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
以下为分析:
dp[j]为 容量为j的背包所背的最大价值。
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 [j - 物品i重量] 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,一个是取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放物品i,一个是取dp[j - weight[i]] + value[i],即放物品i,指定是取最大的,毕竟是求最大价值,
所以递归公式为:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
可以看出相对于二维dp数组的写法,就是把dp[i][j]中i的维度去掉了。
- 一维dp数组如何初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
- 一维dp数组遍历顺序
代码如下:
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
这里大家发现和二维dp的写法中,遍历背包的顺序是不一样的!
二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
为什么呢?
倒序遍历是为了保证物品i只被放入一次!。但如果一旦正序遍历了,那么物品0就会被重复加入多次!
举一个例子:物品0的重量weight[0] = 1,价值value[0] = 15
如果正序遍历
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
此时dp[2]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
为什么倒序遍历,就可以保证物品只放入一次呢?
倒序就是先算dp[2]
dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp数组已经都初始化为0)
dp[1] = dp[1 - weight[0]] + value[0] = 15
所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
那么问题又来了,为什么二维dp数组遍历的时候不用倒序呢?
因为对于二维dp,dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,本层的dp[i][j]并不会被覆盖!
(如何这里读不懂,大家就要动手试一试了,空想还是不靠谱的,实践出真知!)
再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
不可以!
因为一维dp的写法,背包容量一定是要倒序遍历(原因上面已经讲了),如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。
所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的!,这一点大家一定要注意。
- 举例推导dp数组
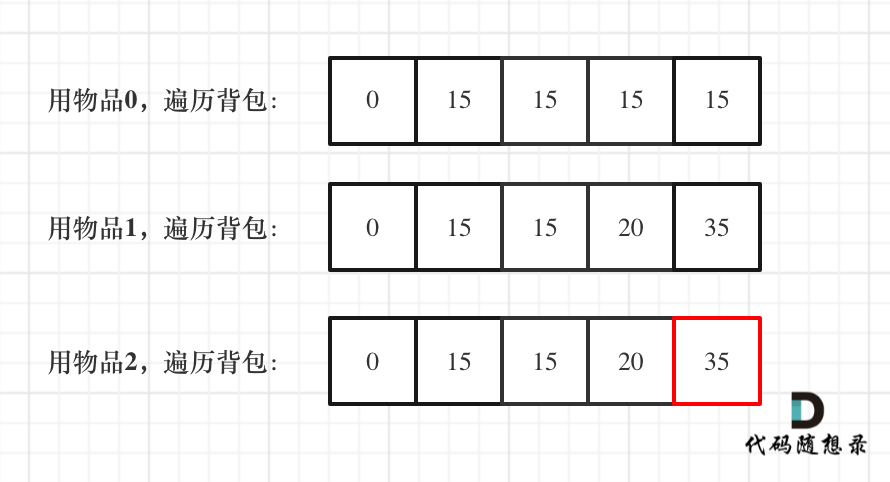
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
本题力扣上没有原题,大家可以去卡码网第46题去练习,题意是一样的,代码如下:
// 一维dp数组实现
#include <iostream>
#include <vector>
using namespace std;
int main() {
// 读取 M 和 N
int M, N;
cin >> M >> N;
vector<int> costs(M);
vector<int> values(M);
for (int i = 0; i < M; i++) {
cin >> costs[i];
}
for (int j = 0; j < M; j++) {
cin >> values[j];
}
// 创建一个动态规划数组dp,初始值为0
vector<int> dp(N + 1, 0);
// 外层循环遍历每个类型的研究材料
for (int i = 0; i < M; ++i) {
// 内层循环从 N 空间逐渐减少到当前研究材料所占空间
for (int j = N; j >= costs[i]; --j) {
// 考虑当前研究材料选择和不选择的情况,选择最大值
dp[j] = max(dp[j], dp[j - costs[i]] + values[i]);
}
}
// 输出dp[N],即在给定 N 行李空间可以携带的研究材料最大价值
cout << dp[N] << endl;
return 0;
}
可以看出,一维dp 的01背包,要比二维简洁的多! 初始化 和 遍历顺序相对简单了。
所以我倾向于使用一维dp数组的写法,比较直观简洁,而且空间复杂度还降了一个数量级!
在后面背包问题的讲解中,我都直接使用一维dp数组来进行推导。
以上的讲解可以开发一道面试题目(毕竟力扣上没原题)。
就是本文中的题目,要求先实现一个纯二维的01背包,如果写出来了,然后再问为什么两个for循环的嵌套顺序这么写?反过来写行不行?再讲一讲初始化的逻辑。
然后要求实现一个一维数组的01背包,最后再问,一维数组的01背包,两个for循环的顺序反过来写行不行?为什么?
注意以上问题都是在候选人把代码写出来的情况下才问的。
就是纯01背包的题目,都不用考01背包应用类的题目就可以看出候选人对算法的理解程度了。
相信大家读完这篇文章,应该对以上问题都有了答案!
此时01背包理论基础就讲完了,我用了两篇文章把01背包的dp数组定义、递推公式、初始化、遍历顺序从二维数组到一维数组统统深度剖析了一遍,没有放过任何难点。
大家可以发现其实信息量还是挺大的。
如果把动态规划:关于01背包问题,你该了解这些!和本篇的内容都理解了,后面我们在做01背包的题目,就会发现非常简单了。
不用再凭感觉或者记忆去写背包,而是有自己的思考,了解其本质,代码的方方面面都在自己的掌控之中。
即使代码没有通过,也会有自己的逻辑去debug,这样就思维清晰了。
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int bagweight = scanner.nextInt();
int[] weight = new int[n];
int[] value = new int[n];
for (int i = 0; i < n; ++i) {
weight[i] = scanner.nextInt();
}
for (int j = 0; j < n; ++j) {
value[j] = scanner.nextInt();
}
int[][] dp = new int[n][bagweight + 1];
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
for (int i = 1; i < n; i++) {
for (int j = 0; j <= bagweight; j++) {
if (j < weight[i]) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
}
System.out.println(dp[n - 1][bagweight]);
}
}n, bagweight = map(int, input().split())
weight = list(map(int, input().split()))
value = list(map(int, input().split()))
dp = [[0] * (bagweight + 1) for _ in range(n)]
for j in range(weight[0], bagweight + 1):
dp[0][j] = value[0]
for i in range(1, n):
for j in range(bagweight + 1):
if j < weight[i]:
dp[i][j] = dp[i - 1][j]
else:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
print(dp[n - 1][bagweight])package main
import (
"fmt"
)
func main() {
var n, bagweight int
fmt.Scan(&n, &bagweight)
weight := make([]int, n)
value := make([]int, n)
for i := 0; i < n; i++ {
fmt.Scan(&weight[i])
}
for j := 0; j < n; j++ {
fmt.Scan(&value[j])
}
dp := make([][]int, n)
for i := range dp {
dp[i] = make([]int, bagweight+1)
}
for j := weight[0]; j <= bagweight; j++ {
dp[0][j] = value[0]
}
for i := 1; i < n; i++ {
for j := 0; j <= bagweight; j++ {
if j < weight[i] {
dp[i][j] = dp[i-1][j]
} else {
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
}
}
}
fmt.Println(dp[n-1][bagweight])
}
func max(a, b int) int {
if a > b {
return a
}
return b
}const readline = require('readline').createInterface({
input: process.stdin,
output: process.stdout
});
let input = [];
readline.on('line', (line) => {
input.push(line);
});
readline.on('close', () => {
let [n, bagweight] = input[0].split(' ').map(Number);
let weight = input[1].split(' ').map(Number);
let value = input[2].split(' ').map(Number);
let dp = Array.from({ length: n }, () => Array(bagweight + 1).fill(0));
for (let j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
for (let i = 1; i < n; i++) {
for (let j = 0; j <= bagweight; j++) {
if (j < weight[i]) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
}
console.log(dp[n - 1][bagweight]);
});
#include <stdio.h>
#include <stdlib.h>
int max(int a, int b) {
return a > b ? a : b;
}
int main() {
int n, bagweight;
scanf("%d %d", &n, &bagweight);
int *weight = (int *)malloc(n * sizeof(int));
int *value = (int *)malloc(n * sizeof(int));
for (int i = 0; i < n; ++i) {
scanf("%d", &weight[i]);
}
for (int j = 0; j < n; ++j) {
scanf("%d", &value[j]);
}
int **dp = (int **)malloc(n * sizeof(int *));
for (int i = 0; i < n; ++i) {
dp[i] = (int *)malloc((bagweight + 1) * sizeof(int));
for (int j = 0; j <= bagweight; ++j) {
dp[i][j] = 0;
}
}
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
for (int i = 1; i < n; i++) {
for (int j = 0; j <= bagweight; j++) {
if (j < weight[i]) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
}
printf("%d\n", dp[n - 1][bagweight]);
for (int i = 0; i < n; ++i) {
free(dp[i]);
}
free(dp);
free(weight);
free(value);
return 0;
}