README.md

comments	difficulty	edit_url	rating	source	tags
true	中等	https://github.com/doocs/leetcode/edit/main/solution/2400-2499/2498.Frog%20Jump%20II/README.md	1759	第 93 场双周赛 Q3	贪心 数组 二分查找

2498. 青蛙过河 II

English Version

题目描述

给你一个下标从 0 开始的整数数组 stones ，数组中的元素 严格递增 ，表示一条河中石头的位置。

一只青蛙一开始在第一块石头上，它想到达最后一块石头，然后回到第一块石头。同时每块石头 至多 到达 一次。

一次跳跃的 长度 是青蛙跳跃前和跳跃后所在两块石头之间的距离。

• 更正式的，如果青蛙从 stones[i] 跳到 stones[j] ，跳跃的长度为 |stones[i] - stones[j]| 。

一条路径的 代价 是这条路径里的 最大跳跃长度 。

请你返回这只青蛙的 最小代价 。

 

示例 1：

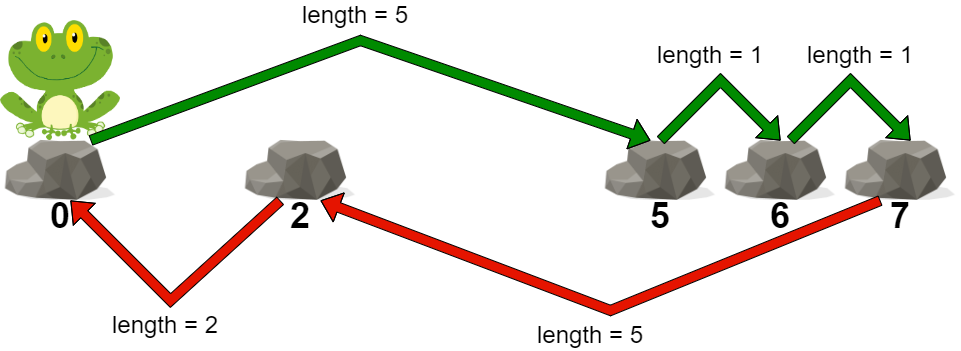
输入：stones = [0,2,5,6,7]
输出：5
解释：上图展示了一条最优路径。
这条路径的代价是 5 ，是这条路径中的最大跳跃长度。
无法得到一条代价小于 5 的路径，我们返回 5 。

示例 2：

输入：stones = [0,3,9]
输出：9
解释：
青蛙可以直接跳到最后一块石头，然后跳回第一块石头。
在这条路径中，每次跳跃长度都是 9 。所以路径代价是 max(9, 9) = 9 。
这是可行路径中的最小代价。

 

提示：

• 2 <= stones.length <= 105
• 0 <= stones[i] <= 109
• stones[0] == 0
• stones 中的元素严格递增。

解法

方法一：脑筋急转弯

要使得跳跃过程中的每一步的最大跳跃长度最小，我们应该将跳跃过程切分成尽可能多的连续的步骤。通过观察，间隔跳跃可以获取最优解。

时间复杂度 $O(n)$，空间复杂度 $O(1)$。其中 $n$ 为数组 stones 的长度。

Python3

class Solution:
    def maxJump(self, stones: List[int]) -> int:
        ans = stones[1] - stones[0]
        for i in range(2, len(stones)):
            ans = max(ans, stones[i] - stones[i - 2])
        return ans

Java

class Solution {
    public int maxJump(int[] stones) {
        int ans = stones[1] - stones[0];
        for (int i = 2; i < stones.length; ++i) {
            ans = Math.max(ans, stones[i] - stones[i - 2]);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int maxJump(vector<int>& stones) {
        int ans = stones[1] - stones[0];
        for (int i = 2; i < stones.size(); ++i) ans = max(ans, stones[i] - stones[i - 2]);
        return ans;
    }
};

Go

func maxJump(stones []int) int {
	ans := stones[1] - stones[0]
	for i := 2; i < len(stones); i++ {
		ans = max(ans, stones[i]-stones[i-2])
	}
	return ans
}