README_EN.md

comments	difficulty	edit_url	rating	source	tags
true	Easy	https://github.com/doocs/leetcode/edit/main/solution/2400-2499/2481.Minimum%20Cuts%20to%20Divide%20a%20Circle/README_EN.md	1246	Biweekly Contest 92 Q1	Geometry Math

2481. Minimum Cuts to Divide a Circle

中文文档

Description

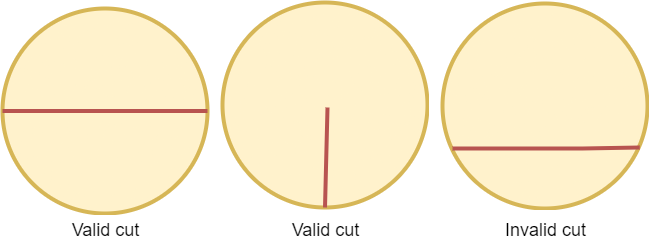
A valid cut in a circle can be:

• A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or
• A cut that is represented by a straight line that touches one point on the edge of the circle and its center.

Some valid and invalid cuts are shown in the figures below.

Given the integer n, return the minimum number of cuts needed to divide a circle into n equal slices.

 

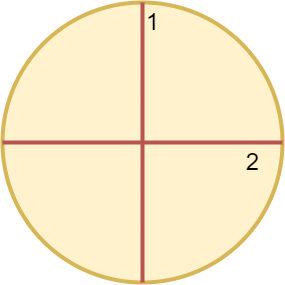
Example 1:

Input: n = 4
Output: 2
Explanation: 
The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices.

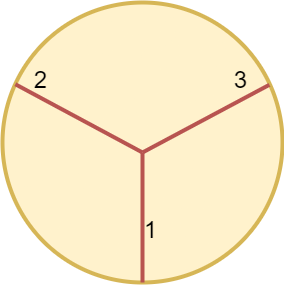
Example 2:

Input: n = 3
Output: 3
Explanation:
At least 3 cuts are needed to divide the circle into 3 equal slices. 
It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape.
Also note that the first cut will not divide the circle into distinct parts.

 

Constraints:

• 1 <= n <= 100

Solutions

Solution 1: Case Discussion

• When $n=1$, no cutting is needed, so the number of cuts is $0$;
• When $n$ is odd, there is no collinear situation, and at least $n$ cuts are needed;
• When $n$ is even, they can be collinear in pairs, and at least $\frac{n}{2}$ cuts are needed.

In summary, we can get:

$$ \textit{ans} = \begin{cases} n, & n \gt 1 \textit{ and } n \textit{ is odd} \\ \frac{n}{2}, & n \textit{ is even} \\ \end{cases} $$

The time complexity is $O(1)$, and the space complexity is $O(1)$.

Python3

class Solution:
    def numberOfCuts(self, n: int) -> int:
        return n if (n > 1 and n & 1) else n >> 1

Java

class Solution {
    public int numberOfCuts(int n) {
        return n > 1 && n % 2 == 1 ? n : n >> 1;
    }
}

C++

class Solution {
public:
    int numberOfCuts(int n) {
        return n > 1 && n % 2 == 1 ? n : n >> 1;
    }
};

Go

func numberOfCuts(n int) int {
	if n > 1 && n%2 == 1 {
		return n
	}
	return n >> 1
}

TypeScript

function numberOfCuts(n: number): number {
    return n > 1 && n & 1 ? n : n >> 1;
}

Rust

impl Solution {
    pub fn number_of_cuts(n: i32) -> i32 {
        if n > 1 && n % 2 == 1 {
            return n;
        }
        n >> 1
    }
}

C#

public class Solution {
    public int NumberOfCuts(int n) {
        return n > 1 && n % 2 == 1 ? n : n >> 1;
    }
}