Skip to content

Latest commit

 

History

History
190 lines (149 loc) · 6.26 KB

README.md

File metadata and controls

190 lines (149 loc) · 6.26 KB
Raw
comments difficulty edit_url rating source tags
true
中等
2021
第 78 场双周赛 Q3
贪心
数组
二分查找
前缀和
排序

2271. 毯子覆盖的最多白色砖块数

English Version

题目描述

给你一个二维整数数组 tiles ，其中 tiles[i] = [li, ri] ，表示所有在 li <= j <= ri 之间的每个瓷砖位置 j 都被涂成了白色。

同时给你一个整数 carpetLen ，表示可以放在 任何位置 的一块毯子的长度。

请你返回使用这块毯子，最多 可以盖住多少块瓷砖。

 

示例 1：

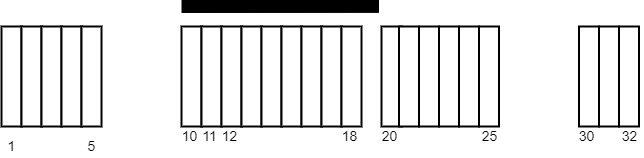
输入：tiles = [[1,5],[10,11],[12,18],[20,25],[30,32]], carpetLen = 10
输出：9
解释：将毯子从瓷砖 10 开始放置。
总共覆盖 9 块瓷砖，所以返回 9 。
注意可能有其他方案也可以覆盖 9 块瓷砖。
可以看出，瓷砖无法覆盖超过 9 块瓷砖。

示例 2：

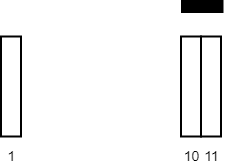
输入：tiles = [[10,11],[1,1]], carpetLen = 2
输出：2
解释：将毯子从瓷砖 10 开始放置。
总共覆盖 2 块瓷砖，所以我们返回 2 。

 

提示：

  • 1 <= tiles.length <= 5 * 104
  • tiles[i].length == 2
  • 1 <= li <= ri <= 109
  • 1 <= carpetLen <= 109
  • tiles 互相 不会重叠 。

解法

方法一：贪心 + 排序 + 滑动窗口

直觉上，毯子的左端点一定与某块瓷砖的左端点重合，这样才能使得毯子覆盖的瓷砖最多。

我们可以来简单证明一下。

如果毯子落在某块瓷砖的中间某个位置，将毯子右移一个，毯子覆盖的瓷砖数量可能减少，也可能不变，但不可能增加；将毯子左移一个，毯子覆盖的瓷砖数量可能不变，也可能增加，但不可能减少。

也就是说，将毯子左移至某块瓷砖的左端点，一定可以使得毯子覆盖的瓷砖数量最多。

因此，我们可以将所有瓷砖按照左端点从小到大排序，然后枚举每块瓷砖的左端点，计算出以该左端点为起点的毯子覆盖的瓷砖数量，取最大值即可。

为了计算以某块瓷砖的左端点为起点的毯子覆盖的瓷砖数量，我们可以使用滑动窗口的思想，维护一个右端点不断右移的窗口，窗口内的瓷砖数量即为毯子覆盖的瓷砖数量。

时间复杂度 $O(n\log n)$，其中 $n$ 为瓷砖的数量。

Python3

class Solution:
    def maximumWhiteTiles(self, tiles: List[List[int]], carpetLen: int) -> int:
        tiles.sort()
        n = len(tiles)
        s = ans = j = 0
        for i, (li, ri) in enumerate(tiles):
            while j < n and tiles[j][1] - li + 1 <= carpetLen:
                s += tiles[j][1] - tiles[j][0] + 1
                j += 1
            if j < n and li + carpetLen > tiles[j][0]:
                ans = max(ans, s + li + carpetLen - tiles[j][0])
            else:
                ans = max(ans, s)
            s -= ri - li + 1
        return ans

Java

class Solution {
    public int maximumWhiteTiles(int[][] tiles, int carpetLen) {
        Arrays.sort(tiles, (a, b) -> a[0] - b[0]);
        int n = tiles.length;
        int s = 0, ans = 0;
        for (int i = 0, j = 0; i < n; ++i) {
            while (j < n && tiles[j][1] - tiles[i][0] + 1 <= carpetLen) {
                s += tiles[j][1] - tiles[j][0] + 1;
                ++j;
            }
            if (j < n && tiles[i][0] + carpetLen > tiles[j][0]) {
                ans = Math.max(ans, s + tiles[i][0] + carpetLen - tiles[j][0]);
            } else {
                ans = Math.max(ans, s);
            }
            s -= (tiles[i][1] - tiles[i][0] + 1);
        }
        return ans;
    }
}

C++

class Solution {
public:
    int maximumWhiteTiles(vector<vector<int>>& tiles, int carpetLen) {
        sort(tiles.begin(), tiles.end());
        int s = 0, ans = 0, n = tiles.size();
        for (int i = 0, j = 0; i < n; ++i) {
            while (j < n && tiles[j][1] - tiles[i][0] + 1 <= carpetLen) {
                s += tiles[j][1] - tiles[j][0] + 1;
                ++j;
            }
            if (j < n && tiles[i][0] + carpetLen > tiles[j][0]) {
                ans = max(ans, s + tiles[i][0] + carpetLen - tiles[j][0]);
            } else {
                ans = max(ans, s);
            }
            s -= (tiles[i][1] - tiles[i][0] + 1);
        }
        return ans;
    }
};

Go

func maximumWhiteTiles(tiles [][]int, carpetLen int) int {
	sort.Slice(tiles, func(i, j int) bool { return tiles[i][0] < tiles[j][0] })
	n := len(tiles)
	s, ans := 0, 0
	for i, j := 0, 0; i < n; i++ {
		for j < n && tiles[j][1]-tiles[i][0]+1 <= carpetLen {
			s += tiles[j][1] - tiles[j][0] + 1
			j++
		}
		if j < n && tiles[i][0]+carpetLen > tiles[j][0] {
			ans = max(ans, s+tiles[i][0]+carpetLen-tiles[j][0])
		} else {
			ans = max(ans, s)
		}
		s -= (tiles[i][1] - tiles[i][0] + 1)
	}
	return ans
}