Skip to content

Latest commit

 

History

History
237 lines (193 loc) · 8.78 KB

README.md

File metadata and controls

237 lines (193 loc) · 8.78 KB
Raw
comments difficulty edit_url rating source tags
true
困难
2413
第 56 场双周赛 Q4
图
数组
动态规划

1928. 规定时间内到达终点的最小花费

English Version

题目描述

一个国家有 n 个城市，城市编号为 0 到 n - 1 ，题目保证 所有城市 都由双向道路 连接在一起 。道路由二维整数数组 edges 表示，其中 edges[i] = [xi, yi, timei] 表示城市 xi 和 yi 之间有一条双向道路，耗费时间为 timei 分钟。两个城市之间可能会有多条耗费时间不同的道路，但是不会有道路两头连接着同一座城市。

每次经过一个城市时，你需要付通行费。通行费用一个长度为 n 且下标从 0 开始的整数数组 passingFees 表示，其中 passingFees[j] 是你经过城市 j 需要支付的费用。

一开始，你在城市 0 ，你想要在 maxTime 分钟以内 （包含 maxTime 分钟）到达城市 n - 1 。旅行的 费用 为你经过的所有城市 通行费之和 （包括 起点和终点城市的通行费）。

给你 maxTime，edges 和 passingFees ，请你返回完成旅行的 最小费用 ，如果无法在 maxTime 分钟以内完成旅行，请你返回 -1 。

 

示例 1：

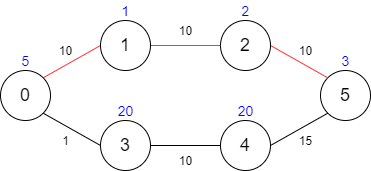
输入：maxTime = 30, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：11
解释：最优路径为 0 -> 1 -> 2 -> 5 ，总共需要耗费 30 分钟，需要支付 11 的通行费。

示例 2：

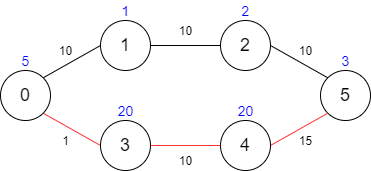
输入：maxTime = 29, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：48
解释：最优路径为 0 -> 3 -> 4 -> 5 ，总共需要耗费 26 分钟，需要支付 48 的通行费。
你不能选择路径 0 -> 1 -> 2 -> 5 ，因为这条路径耗费的时间太长。

示例 3：

输入：maxTime = 25, edges = [[0,1,10],[1,2,10],[2,5,10],[0,3,1],[3,4,10],[4,5,15]], passingFees = [5,1,2,20,20,3]
输出：-1
解释：无法在 25 分钟以内从城市 0 到达城市 5 。

 

提示：

  • 1 <= maxTime <= 1000
  • n == passingFees.length
  • 2 <= n <= 1000
  • n - 1 <= edges.length <= 1000
  • 0 <= xi, yi <= n - 1
  • 1 <= timei <= 1000
  • 1 <= passingFees[j] <= 1000 
  • 图中两个节点之间可能有多条路径。
  • 图中不含有自环。

解法

方法一：动态规划

我们定义 $f[i][j]$ 表示经过 $i$ 分钟，从城市 $0$ 到达城市 $j$ 的最小花费。初始时 $f[0][0] = \textit{passingFees}[0]$，其余的 $f[0][j] = +\infty$。

接下来，我们在 $[1, \textit{maxTime}]$ 的时间范围内，遍历所有的边，对于每一条边 $(x, y, t)$，如果 $t \leq i$，那么我们：

  • 可以先经过 $i - t$ 分钟，从城市 $0$ 到达城市 $y$，然后再经过 $t$ 分钟，从城市 $y$ 到达城市 $x$，再加上到达城市 $x$ 的通行费，即 $f[i][x] = \min(f[i][x], f[i - t][y] + \textit{passingFees}[x])$；
  • 也可以先经过 $i - t$ 分钟，从城市 $0$ 到达城市 $x$，然后再经过 $t$ 分钟，从城市 $x$ 到达城市 $y$，再加上到达城市 $y$ 的通行费，即 $f[i][y] = \min(f[i][y], f[i - t][x] + \textit{passingFees}[y])$。

最终答案即为 $\min{f[i][n - 1]}$，其中 $i \in [0, \textit{maxTime}]$。如果答案为 $+\infty$，则返回 $-1$。

时间复杂度 $O(\textit{maxTime} \times (m + n))$，其中 $m$ 和 $n$ 分别是边的数量和城市的数量。空间复杂度 $O(\textit{maxTime} \times n)$。

Python3

class Solution:
    def minCost(
        self, maxTime: int, edges: List[List[int]], passingFees: List[int]
    ) -> int:
        m, n = maxTime, len(passingFees)
        f = [[inf] * n for _ in range(m + 1)]
        f[0][0] = passingFees[0]
        for i in range(1, m + 1):
            for x, y, t in edges:
                if t <= i:
                    f[i][x] = min(f[i][x], f[i - t][y] + passingFees[x])
                    f[i][y] = min(f[i][y], f[i - t][x] + passingFees[y])
        ans = min(f[i][n - 1] for i in range(m + 1))
        return ans if ans < inf else -1

Java

class Solution {
    public int minCost(int maxTime, int[][] edges, int[] passingFees) {
        int m = maxTime, n = passingFees.length;
        int[][] f = new int[m + 1][n];
        final int inf = 1 << 30;
        for (var g : f) {
            Arrays.fill(g, inf);
        }
        f[0][0] = passingFees[0];
        for (int i = 1; i <= m; ++i) {
            for (var e : edges) {
                int x = e[0], y = e[1], t = e[2];
                if (t <= i) {
                    f[i][x] = Math.min(f[i][x], f[i - t][y] + passingFees[x]);
                    f[i][y] = Math.min(f[i][y], f[i - t][x] + passingFees[y]);
                }
            }
        }
        int ans = inf;
        for (int i = 0; i <= m; ++i) {
            ans = Math.min(ans, f[i][n - 1]);
        }
        return ans == inf ? -1 : ans;
    }
}

C++

class Solution {
public:
    int minCost(int maxTime, vector<vector<int>>& edges, vector<int>& passingFees) {
        int m = maxTime, n = passingFees.size();
        const int inf = 1 << 30;
        vector<vector<int>> f(m + 1, vector<int>(n, inf));
        f[0][0] = passingFees[0];
        for (int i = 1; i <= m; ++i) {
            for (const auto& e : edges) {
                int x = e[0], y = e[1], t = e[2];
                if (t <= i) {
                    f[i][x] = min(f[i][x], f[i - t][y] + passingFees[x]);
                    f[i][y] = min(f[i][y], f[i - t][x] + passingFees[y]);
                }
            }
        }
        int ans = inf;
        for (int i = 1; i <= m; ++i) {
            ans = min(ans, f[i][n - 1]);
        }
        return ans == inf ? -1 : ans;
    }
};

Go

func minCost(maxTime int, edges [][]int, passingFees []int) int {
	m, n := maxTime, len(passingFees)
	f := make([][]int, m+1)
	const inf int = 1 << 30
	for i := range f {
		f[i] = make([]int, n)
		for j := range f[i] {
			f[i][j] = inf
		}
	}
	f[0][0] = passingFees[0]
	for i := 1; i <= m; i++ {
		for _, e := range edges {
			x, y, t := e[0], e[1], e[2]
			if t <= i {
				f[i][x] = min(f[i][x], f[i-t][y]+passingFees[x])
				f[i][y] = min(f[i][y], f[i-t][x]+passingFees[y])
			}
		}
	}
	ans := inf
	for i := 1; i <= m; i++ {
		ans = min(ans, f[i][n-1])
	}
	if ans == inf {
		return -1
	}
	return ans
}

TypeScript

function minCost(maxTime: number, edges: number[][], passingFees: number[]): number {
    const [m, n] = [maxTime, passingFees.length];
    const f: number[][] = Array.from({ length: m + 1 }, () => Array(n).fill(Infinity));
    f[0][0] = passingFees[0];
    for (let i = 1; i <= m; ++i) {
        for (const [x, y, t] of edges) {
            if (t <= i) {
                f[i][x] = Math.min(f[i][x], f[i - t][y] + passingFees[x]);
                f[i][y] = Math.min(f[i][y], f[i - t][x] + passingFees[y]);
            }
        }
    }
    let ans = Infinity;
    for (let i = 1; i <= m; ++i) {
        ans = Math.min(ans, f[i][n - 1]);
    }
    return ans === Infinity ? -1 : ans;
}