Skip to content

Latest commit

 

History

History
371 lines (299 loc) · 11.9 KB

README.md

File metadata and controls

371 lines (299 loc) · 11.9 KB
Raw
comments difficulty edit_url rating source tags
true
困难
2040
第 45 场双周赛 Q4
数组
二分查找
动态规划
排序

1751. 最多可以参加的会议数目 II

English Version

题目描述

给你一个 events 数组，其中 events[i] = [startDayi, endDayi, valuei] ，表示第 i 个会议在 startDayi 天开始，第 endDayi 天结束，如果你参加这个会议，你能得到价值 valuei 。同时给你一个整数 k 表示你能参加的最多会议数目。

你同一时间只能参加一个会议。如果你选择参加某个会议，那么你必须 完整 地参加完这个会议。会议结束日期是包含在会议内的，也就是说你不能同时参加一个开始日期与另一个结束日期相同的两个会议。

请你返回能得到的会议价值 最大和 。

 

示例 1：

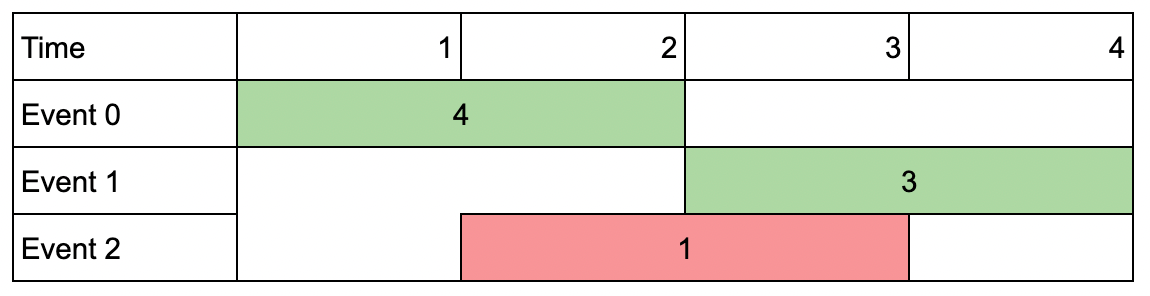
输入：events = [[1,2,4],[3,4,3],[2,3,1]], k = 2
输出：7
解释：选择绿色的活动会议 0 和 1，得到总价值和为 4 + 3 = 7 。

示例 2：

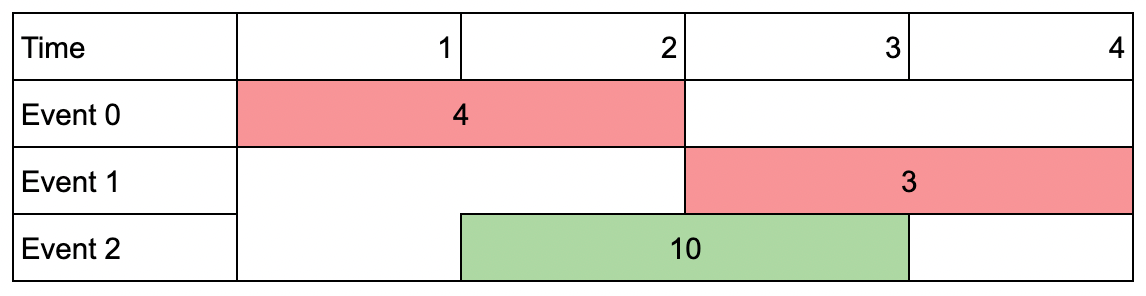
输入：events = [[1,2,4],[3,4,3],[2,3,10]], k = 2
输出：10
解释：参加会议 2 ，得到价值和为 10 。
你没法再参加别的会议了，因为跟会议 2 有重叠。你 不 需要参加满 k 个会议。

示例 3：

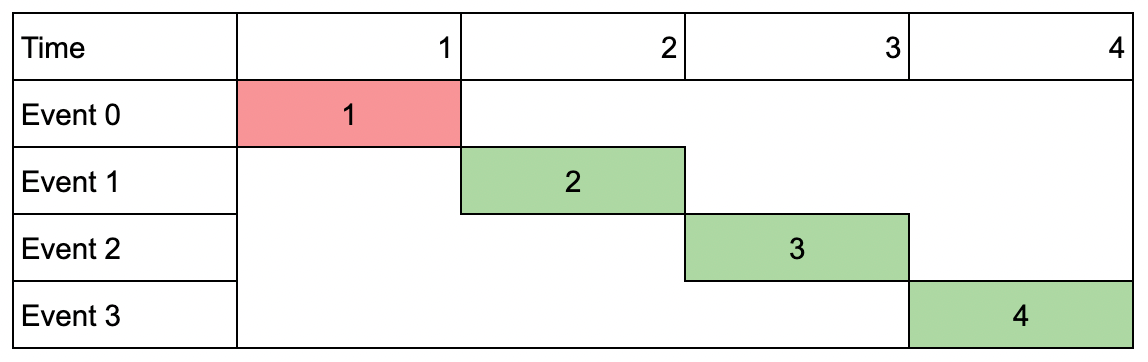
输入：events = [[1,1,1],[2,2,2],[3,3,3],[4,4,4]], k = 3
输出：9
解释：尽管会议互不重叠，你只能参加 3 个会议，所以选择价值最大的 3 个会议。

 

提示：

  • 1 <= k <= events.length
  • 1 <= k * events.length <= 106
  • 1 <= startDayi <= endDayi <= 109
  • 1 <= valuei <= 106

解法

方法一：记忆化搜索 + 二分查找

我们先将会议按照开始时间从小到大排序，然后设计一个函数 $dfs(i, k)$ 表示从第 $i$ 个会议开始，最多参加 $k$ 个会议的最大价值和。答案即为 $dfs(0, k)$。

函数 $dfs(i, k)$ 的计算过程如下：

对于第 $i$ 个会议，我们可以选择参加或者不参加。如果不参加，那么最大价值和就是 $dfs(i + 1, k)$，如果参加，我们可以通过二分查找，找到第一个开始时间大于第 $i$ 个会议结束时间的会议，记为 $j$，那么最大价值和就是 $dfs(j, k - 1) + value[i]$。取二者的较大值即可。即：

$$ dfs(i, k) = \max(dfs(i + 1, k), dfs(j, k - 1) + value[i]) $$

其中 $j$ 为第一个开始时间大于第 $i$ 个会议结束时间的会议，可以通过二分查找得到。

由于函数 $dfs(i, k)$ 的计算过程中，会调用 $dfs(i + 1, k)$ 和 $dfs(j, k - 1)$，因此我们可以使用记忆化搜索，将计算过的值保存下来，避免重复计算。

时间复杂度 $O(n\times \log n + n\times k)$，其中 $n$ 为会议数量。

Python3

class Solution:
    def maxValue(self, events: List[List[int]], k: int) -> int:
        @cache
        def dfs(i: int, k: int) -> int:
            if i >= len(events):
                return 0
            _, ed, val = events[i]
            ans = dfs(i + 1, k)
            if k:
                j = bisect_right(events, ed, lo=i + 1, key=lambda x: x[0])
                ans = max(ans, dfs(j, k - 1) + val)
            return ans

        events.sort()
        return dfs(0, k)

Java

class Solution {
    private int[][] events;
    private int[][] f;
    private int n;

    public int maxValue(int[][] events, int k) {
        Arrays.sort(events, (a, b) -> a[0] - b[0]);
        this.events = events;
        n = events.length;
        f = new int[n][k + 1];
        return dfs(0, k);
    }

    private int dfs(int i, int k) {
        if (i >= n || k <= 0) {
            return 0;
        }
        if (f[i][k] != 0) {
            return f[i][k];
        }
        int j = search(events, events[i][1], i + 1);
        int ans = Math.max(dfs(i + 1, k), dfs(j, k - 1) + events[i][2]);
        return f[i][k] = ans;
    }

    private int search(int[][] events, int x, int lo) {
        int l = lo, r = n;
        while (l < r) {
            int mid = (l + r) >> 1;
            if (events[mid][0] > x) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return l;
    }
}

C++

class Solution {
public:
    int maxValue(vector<vector<int>>& events, int k) {
        sort(events.begin(), events.end());
        int n = events.size();
        int f[n][k + 1];
        memset(f, 0, sizeof(f));
        function<int(int, int)> dfs = [&](int i, int k) -> int {
            if (i >= n || k <= 0) {
                return 0;
            }
            if (f[i][k] > 0) {
                return f[i][k];
            }
            int ed = events[i][1], val = events[i][2];
            vector<int> t = {ed};
            int p = upper_bound(events.begin() + i + 1, events.end(), t, [](const auto& a, const auto& b) { return a[0] < b[0]; }) - events.begin();
            f[i][k] = max(dfs(i + 1, k), dfs(p, k - 1) + val);
            return f[i][k];
        };
        return dfs(0, k);
    }
};

Go

func maxValue(events [][]int, k int) int {
	sort.Slice(events, func(i, j int) bool { return events[i][0] < events[j][0] })
	n := len(events)
	f := make([][]int, n)
	for i := range f {
		f[i] = make([]int, k+1)
	}
	var dfs func(i, k int) int
	dfs = func(i, k int) int {
		if i >= n || k <= 0 {
			return 0
		}
		if f[i][k] > 0 {
			return f[i][k]
		}
		j := sort.Search(n, func(h int) bool { return events[h][0] > events[i][1] })
		ans := max(dfs(i+1, k), dfs(j, k-1)+events[i][2])
		f[i][k] = ans
		return ans
	}
	return dfs(0, k)
}

TypeScript

function maxValue(events: number[][], k: number): number {
    events.sort((a, b) => a[1] - b[1]);
    const n = events.length;
    const f: number[][] = new Array(n + 1).fill(0).map(() => new Array(k + 1).fill(0));
    const search = (x: number, hi: number): number => {
        let l = 0;
        let r = hi;
        while (l < r) {
            const mid = (l + r) >> 1;
            if (events[mid][1] >= x) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return l;
    };
    for (let i = 1; i <= n; ++i) {
        const [st, _, val] = events[i - 1];
        const p = search(st, i - 1);
        for (let j = 1; j <= k; ++j) {
            f[i][j] = Math.max(f[i - 1][j], f[p][j - 1] + val);
        }
    }
    return f[n][k];
}

方法二：动态规划 + 二分查找

我们可以将方法一中的记忆化搜索改为动态规划。

先将会议排序，这次我们按照结束时间从小到大排序。然后定义 $f[i][j]$ 表示前 $i$ 个会议中，最多参加 $j$ 个会议的最大价值和。答案即为 $f[n][k]$。

对于第 $i$ 个会议，我们可以选择参加或者不参加。如果不参加，那么最大价值和就是 $f[i][j]$，如果参加，我们可以通过二分查找，找到最后一个结束时间小于第 $i$ 个会议开始时间的会议，记为 $h$，那么最大价值和就是 $f[h+1][j - 1] + value[i]$。取二者的较大值即可。即：

$$ f[i+1][j] = \max(f[i][j], f[h+1][j - 1] + value[i]) $$

其中 $h$ 为最后一个结束时间小于第 $i$ 个会议开始时间的会议，可以通过二分查找得到。

时间复杂度 $O(n\times \log n + n\times k)$，其中 $n$ 为会议数量。

相似题目：

Python3

class Solution:
    def maxValue(self, events: List[List[int]], k: int) -> int:
        events.sort(key=lambda x: x[1])
        n = len(events)
        f = [[0] * (k + 1) for _ in range(n + 1)]
        for i, (st, _, val) in enumerate(events, 1):
            p = bisect_left(events, st, hi=i - 1, key=lambda x: x[1])
            for j in range(1, k + 1):
                f[i][j] = max(f[i - 1][j], f[p][j - 1] + val)
        return f[n][k]

Java

class Solution {
    public int maxValue(int[][] events, int k) {
        Arrays.sort(events, (a, b) -> a[1] - b[1]);
        int n = events.length;
        int[][] f = new int[n + 1][k + 1];
        for (int i = 1; i <= n; ++i) {
            int st = events[i - 1][0], val = events[i - 1][2];
            int p = search(events, st, i - 1);
            for (int j = 1; j <= k; ++j) {
                f[i][j] = Math.max(f[i - 1][j], f[p][j - 1] + val);
            }
        }
        return f[n][k];
    }

    private int search(int[][] events, int x, int hi) {
        int l = 0, r = hi;
        while (l < r) {
            int mid = (l + r) >> 1;
            if (events[mid][1] >= x) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return l;
    }
}

C++

class Solution {
public:
    int maxValue(vector<vector<int>>& events, int k) {
        sort(events.begin(), events.end(), [](const auto& a, const auto& b) { return a[1] < b[1]; });
        int n = events.size();
        int f[n + 1][k + 1];
        memset(f, 0, sizeof(f));
        for (int i = 1; i <= n; ++i) {
            int st = events[i - 1][0], val = events[i - 1][2];
            vector<int> t = {st};
            int p = lower_bound(events.begin(), events.begin() + i - 1, t, [](const auto& a, const auto& b) { return a[1] < b[0]; }) - events.begin();
            for (int j = 1; j <= k; ++j) {
                f[i][j] = max(f[i - 1][j], f[p][j - 1] + val);
            }
        }
        return f[n][k];
    }
};

Go

func maxValue(events [][]int, k int) int {
	sort.Slice(events, func(i, j int) bool { return events[i][1] < events[j][1] })
	n := len(events)
	f := make([][]int, n+1)
	for i := range f {
		f[i] = make([]int, k+1)
	}
	for i := 1; i <= n; i++ {
		st, val := events[i-1][0], events[i-1][2]
		p := sort.Search(i, func(j int) bool { return events[j][1] >= st })
		for j := 1; j <= k; j++ {
			f[i][j] = max(f[i-1][j], f[p][j-1]+val)
		}
	}
	return f[n][k]
}