Skip to content

Latest commit

 

History

History
713 lines (634 loc) · 23.3 KB

README.md

File metadata and controls

713 lines (634 loc) · 23.3 KB
Raw
comments difficulty edit_url rating source tags
true
困难
2655
第 215 场周赛 Q4
位运算
记忆化搜索
动态规划
状态压缩

1659. 最大化网格幸福感

English Version

题目描述

给你四个整数 m、n、introvertsCount 和 extrovertsCount 。有一个 m x n 网格，和两种类型的人：内向的人和外向的人。总共有 introvertsCount 个内向的人和 extrovertsCount 个外向的人。

请你决定网格中应当居住多少人，并为每个人分配一个网格单元。 注意，不必 让所有人都生活在网格中。

每个人的 幸福感 计算如下：

  • 内向的人 开始 时有 120 个幸福感，但每存在一个邻居（内向的或外向的）他都会 失去  30 个幸福感。
  • 外向的人 开始 时有 40 个幸福感，每存在一个邻居（内向的或外向的）他都会 得到  20 个幸福感。

邻居是指居住在一个人所在单元的上、下、左、右四个直接相邻的单元中的其他人。

网格幸福感 是每个人幸福感的 总和 。 返回 最大可能的网格幸福感 。

 

示例 1：

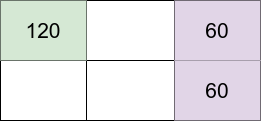
输入：m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2
输出：240
解释：假设网格坐标 (row, column) 从 1 开始编号。
将内向的人放置在单元 (1,1) ，将外向的人放置在单元 (1,3) 和 (2,3) 。
- 位于 (1,1) 的内向的人的幸福感：120（初始幸福感）- (0 * 30)（0 位邻居）= 120
- 位于 (1,3) 的外向的人的幸福感：40（初始幸福感）+ (1 * 20)（1 位邻居）= 60
- 位于 (2,3) 的外向的人的幸福感：40（初始幸福感）+ (1 * 20)（1 位邻居）= 60
网格幸福感为：120 + 60 + 60 = 240
上图展示该示例对应网格中每个人的幸福感。内向的人在浅绿色单元中，而外向的人在浅紫色单元中。

示例 2：

输入：m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1
输出：260
解释：将内向的人放置在单元 (1,1) 和 (3,1) ，将外向的人放置在单元 (2,1) 。
- 位于 (1,1) 的内向的人的幸福感：120（初始幸福感）- (1 * 30)（1 位邻居）= 90
- 位于 (2,1) 的外向的人的幸福感：40（初始幸福感）+ (2 * 20)（2 位邻居）= 80
- 位于 (3,1) 的内向的人的幸福感：120（初始幸福感）- (1 * 30)（1 位邻居）= 90
网格幸福感为 90 + 80 + 90 = 260

示例 3：

输入：m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0
输出：240

 

提示：

  • 1 <= m, n <= 5
  • 0 <= introvertsCount, extrovertsCount <= min(m * n, 6)

解法

方法一：三进制状态压缩 + 记忆化搜索

我们注意到，题目中 $1 \leq m, n \leq 5$，并且每个网格单元只有三种状态，即：不分配人员、分配内向的人、分配外向的人。因此，我们可以用 $0$, $1$, $2$ 表示这三种状态，网格中的每一行可以用一个长度为 $n$ 的三进制数表示。

我们定义一个函数 $dfs(i, pre, ic, ec)$，表示当前从第 $i$ 行开始，且上一行的状态为 $pre$，内向的人还剩 $ic$ 个，外向的人还剩 $ec$ 个时，网格的最大幸福感。那么答案就是 $dfs(0, 0, introvertsCount, extrovertsCount)$。

函数 $dfs(i, pre, ic, ec)$ 的计算过程如下：

如果 $i = m$，表示已经处理完了所有的行，那么返回 $0$；

如果 $ic = 0$ 且 $ec = 0$，表示所有的人都已经分配完了，那么返回 $0$；

否则，枚举当前行的状态 $cur$，其中 $cur \in [0, 3^n)$，然后计算当前行的幸福感 $f[cur]$，以及与上一行的状态 $pre$ 之间对幸福感的贡献 $g[pre][cur]$，并递归计算 $dfs(i + 1, cur, ic - ix[cur], ec - ex[cur])$，最后返回 $f[cur] + g[pre][cur] + dfs(i + 1, cur, ic - ix[cur], ec - ex[cur])$ 的最大值，即：

$$ dfs(i, pre, ic, ec) = \max_{cur} {f[cur] + g[pre][cur] + dfs(i + 1, cur, ic - ix[cur], ec - ex[cur])} $$

其中：

  • $ix[cur]$ 表示状态 $cur$ 中内向的人的个数；
  • $ex[cur]$ 表示状态 $cur$ 中外向的人的个数；
  • $f[cur]$ 表示状态 $cur$ 中的人的初始幸福感；
  • $g[pre][cur]$ 表示两个相邻状态行对幸福感的贡献。

这些值都可以通过预处理得到。并且，我们可以使用记忆化搜索的方法，避免重复计算。

时间复杂度 $O(3^{2n} \times (m \times ic \times ec + n))$，空间复杂度 $O(3^{2n} + 3^n \times m \times ic \times ec)$。其中 $ic$ 和 $ec$ 分别表示内向的人和外向的人的个数。

Python3

class Solution:
    def getMaxGridHappiness(
        self, m: int, n: int, introvertsCount: int, extrovertsCount: int
    ) -> int:
        @cache
        def dfs(i: int, pre: int, ic: int, ec: int) -> int:
            if i == m or (ic == 0 and ec == 0):
                return 0
            ans = 0
            for cur in range(mx):
                if ix[cur] <= ic and ex[cur] <= ec:
                    a = f[cur] + g[pre][cur]
                    b = dfs(i + 1, cur, ic - ix[cur], ec - ex[cur])
                    ans = max(ans, a + b)
            return ans

        mx = pow(3, n)
        f = [0] * mx
        g = [[0] * mx for _ in range(mx)]
        h = [[0, 0, 0], [0, -60, -10], [0, -10, 40]]
        bits = [[0] * n for _ in range(mx)]
        ix = [0] * mx
        ex = [0] * mx
        for i in range(mx):
            mask = i
            for j in range(n):
                mask, x = divmod(mask, 3)
                bits[i][j] = x
                if x == 1:
                    ix[i] += 1
                    f[i] += 120
                elif x == 2:
                    ex[i] += 1
                    f[i] += 40
                if j:
                    f[i] += h[x][bits[i][j - 1]]
        for i in range(mx):
            for j in range(mx):
                for k in range(n):
                    g[i][j] += h[bits[i][k]][bits[j][k]]
        return dfs(0, 0, introvertsCount, extrovertsCount)

Java

class Solution {
    private int m;
    private int mx;
    private int[] f;
    private int[][] g;
    private int[][] bits;
    private int[] ix;
    private int[] ex;
    private Integer[][][][] memo;
    private final int[][] h = {{0, 0, 0}, {0, -60, -10}, {0, -10, 40}};

    public int getMaxGridHappiness(int m, int n, int introvertsCount, int extrovertsCount) {
        this.m = m;
        mx = (int) Math.pow(3, n);
        f = new int[mx];
        g = new int[mx][mx];
        bits = new int[mx][n];
        ix = new int[mx];
        ex = new int[mx];
        memo = new Integer[m][mx][introvertsCount + 1][extrovertsCount + 1];
        for (int i = 0; i < mx; ++i) {
            int mask = i;
            for (int j = 0; j < n; ++j) {
                int x = mask % 3;
                mask /= 3;
                bits[i][j] = x;
                if (x == 1) {
                    ix[i]++;
                    f[i] += 120;
                } else if (x == 2) {
                    ex[i]++;
                    f[i] += 40;
                }
                if (j > 0) {
                    f[i] += h[x][bits[i][j - 1]];
                }
            }
        }
        for (int i = 0; i < mx; ++i) {
            for (int j = 0; j < mx; ++j) {
                for (int k = 0; k < n; ++k) {
                    g[i][j] += h[bits[i][k]][bits[j][k]];
                }
            }
        }
        return dfs(0, 0, introvertsCount, extrovertsCount);
    }

    private int dfs(int i, int pre, int ic, int ec) {
        if (i == m || (ic == 0 && ec == 0)) {
            return 0;
        }
        if (memo[i][pre][ic][ec] != null) {
            return memo[i][pre][ic][ec];
        }
        int ans = 0;
        for (int cur = 0; cur < mx; ++cur) {
            if (ix[cur] <= ic && ex[cur] <= ec) {
                ans = Math.max(
                    ans, f[cur] + g[pre][cur] + dfs(i + 1, cur, ic - ix[cur], ec - ex[cur]));
            }
        }
        return memo[i][pre][ic][ec] = ans;
    }
}

C++

class Solution {
public:
    int getMaxGridHappiness(int m, int n, int introvertsCount, int extrovertsCount) {
        int mx = pow(3, n);
        int f[mx];
        int g[mx][mx];
        int bits[mx][n];
        int ix[mx];
        int ex[mx];
        int memo[m][mx][introvertsCount + 1][extrovertsCount + 1];
        int h[3][3] = {{0, 0, 0}, {0, -60, -10}, {0, -10, 40}};
        memset(f, 0, sizeof(f));
        memset(g, 0, sizeof(g));
        memset(bits, 0, sizeof(bits));
        memset(ix, 0, sizeof(ix));
        memset(ex, 0, sizeof(ex));
        memset(memo, -1, sizeof(memo));
        for (int i = 0; i < mx; ++i) {
            int mask = i;
            for (int j = 0; j < n; ++j) {
                int x = mask % 3;
                mask /= 3;
                bits[i][j] = x;
                if (x == 1) {
                    ix[i]++;
                    f[i] += 120;
                } else if (x == 2) {
                    ex[i]++;
                    f[i] += 40;
                }
                if (j) {
                    f[i] += h[x][bits[i][j - 1]];
                }
            }
        }
        for (int i = 0; i < mx; ++i) {
            for (int j = 0; j < mx; ++j) {
                for (int k = 0; k < n; ++k) {
                    g[i][j] += h[bits[i][k]][bits[j][k]];
                }
            }
        }
        function<int(int, int, int, int)> dfs = [&](int i, int pre, int ic, int ec) {
            if (i == m || (ic == 0 && ec == 0)) {
                return 0;
            }
            if (memo[i][pre][ic][ec] != -1) {
                return memo[i][pre][ic][ec];
            }
            int ans = 0;
            for (int cur = 0; cur < mx; ++cur) {
                if (ix[cur] <= ic && ex[cur] <= ec) {
                    ans = max(ans, f[cur] + g[pre][cur] + dfs(i + 1, cur, ic - ix[cur], ec - ex[cur]));
                }
            }
            return memo[i][pre][ic][ec] = ans;
        };
        return dfs(0, 0, introvertsCount, extrovertsCount);
    }
};

Go

func getMaxGridHappiness(m int, n int, introvertsCount int, extrovertsCount int) int {
	mx := int(math.Pow(3, float64(n)))
	f := make([]int, mx)
	g := make([][]int, mx)
	h := [3][3]int{{0, 0, 0}, {0, -60, -10}, {0, -10, 40}}
	bits := make([][]int, mx)
	ix := make([]int, mx)
	ex := make([]int, mx)
	memo := make([][][][]int, m)
	for i := range g {
		g[i] = make([]int, mx)
		bits[i] = make([]int, n)
	}
	for i := range memo {
		memo[i] = make([][][]int, mx)
		for j := range memo[i] {
			memo[i][j] = make([][]int, introvertsCount+1)
			for k := range memo[i][j] {
				memo[i][j][k] = make([]int, extrovertsCount+1)
				for l := range memo[i][j][k] {
					memo[i][j][k][l] = -1
				}
			}
		}
	}
	for i := 0; i < mx; i++ {
		mask := i
		for j := 0; j < n; j++ {
			x := mask % 3
			mask /= 3
			bits[i][j] = x
			if x == 1 {
				ix[i]++
				f[i] += 120
			} else if x == 2 {
				ex[i]++
				f[i] += 40
			}
			if j > 0 {
				f[i] += h[x][bits[i][j-1]]
			}
		}
	}
	for i := 0; i < mx; i++ {
		for j := 0; j < mx; j++ {
			for k := 0; k < n; k++ {
				g[i][j] += h[bits[i][k]][bits[j][k]]
			}
		}
	}
	var dfs func(int, int, int, int) int
	dfs = func(i, pre, ic, ec int) int {
		if i == m || (ic == 0 && ec == 0) {
			return 0
		}
		if memo[i][pre][ic][ec] != -1 {
			return memo[i][pre][ic][ec]
		}
		ans := 0
		for cur := 0; cur < mx; cur++ {
			if ix[cur] <= ic && ex[cur] <= ec {
				ans = max(ans, f[cur]+g[pre][cur]+dfs(i+1, cur, ic-ix[cur], ec-ex[cur]))
			}
		}
		memo[i][pre][ic][ec] = ans
		return ans
	}
	return dfs(0, 0, introvertsCount, extrovertsCount)
}

TypeScript

function getMaxGridHappiness(
    m: number,
    n: number,
    introvertsCount: number,
    extrovertsCount: number,
): number {
    const mx = 3 ** n;
    const f: number[] = Array(mx).fill(0);
    const g: number[][] = Array(mx)
        .fill(0)
        .map(() => Array(mx).fill(0));
    const h: number[][] = [
        [0, 0, 0],
        [0, -60, -10],
        [0, -10, 40],
    ];
    const bits: number[][] = Array(mx)
        .fill(0)
        .map(() => Array(n).fill(0));
    const ix: number[] = Array(mx).fill(0);
    const ex: number[] = Array(mx).fill(0);
    const memo: number[][][][] = Array(m)
        .fill(0)
        .map(() =>
            Array(mx)
                .fill(0)
                .map(() =>
                    Array(introvertsCount + 1)
                        .fill(0)
                        .map(() => Array(extrovertsCount + 1).fill(-1)),
                ),
        );
    for (let i = 0; i < mx; ++i) {
        let mask = i;
        for (let j = 0; j < n; ++j) {
            const x = mask % 3;
            mask = Math.floor(mask / 3);
            bits[i][j] = x;
            if (x === 1) {
                ix[i] += 1;
                f[i] += 120;
            } else if (x === 2) {
                ex[i] += 1;
                f[i] += 40;
            }
            if (j > 0) {
                f[i] += h[x][bits[i][j - 1]];
            }
        }
    }
    for (let i = 0; i < mx; ++i) {
        for (let j = 0; j < mx; ++j) {
            for (let k = 0; k < n; ++k) {
                g[i][j] += h[bits[i][k]][bits[j][k]];
            }
        }
    }
    const dfs = (i: number, pre: number, ic: number, ec: number): number => {
        if (i === m || (ic === 0 && ec === 0)) {
            return 0;
        }
        if (memo[i][pre][ic][ec] !== -1) {
            return memo[i][pre][ic][ec];
        }
        let ans = 0;
        for (let cur = 0; cur < mx; ++cur) {
            if (ix[cur] <= ic && ex[cur] <= ec) {
                const a = f[cur] + g[pre][cur];
                const b = dfs(i + 1, cur, ic - ix[cur], ec - ex[cur]);
                ans = Math.max(ans, a + b);
            }
        }
        return (memo[i][pre][ic][ec] = ans);
    };
    return dfs(0, 0, introvertsCount, extrovertsCount);
}

方法二：轮廓线记忆化搜索

我们可以考虑搜索每个网格单元，每次搜索一个位置 $(i, j)$，我们记 $pos = i \times n + j$。那么它左边以及上边的相邻网格会影响到它们之间的幸福感贡献。

我们定义一个函数 $dfs(pos, pre, ic, ec)$，表示当前搜索到位置 $pos$，且此前的 $n$ 个网格单元的状态为 $pre$，内向的人还剩 $ic$ 个，外向的人还剩 $ec$ 个时，网格的最大幸福感。那么答案就是 $dfs(0, 0, introvertsCount, extrovertsCount)$。

函数 $dfs(pos, pre, ic, ec)$ 的计算过程如下：

如果 $pos = m \times n$，表示已经处理完了所有的网格单元，那么返回 $0$；

如果 $ic = 0$ 且 $ec = 0$，表示所有的人都已经分配完了，那么返回 $0$；

否则，我们根据 $pre$ 算出当前网格单元的上边相邻网格单元的状态 $up = \frac{pre}{3^{n-1}}$，以及左边相邻网格单元的状态 $left = pre \bmod 3$（注意，如果 $pos$ 在第 $0$ 列，那么 $left = 0$）。

接下来，我们枚举当前网格单元的状态 $i$，其中 $i \in [0, 3)$。那么当前的 $n$ 个网格单元的状态为 $cur = pre \bmod 3^{n-1} \times 3 + i$，当前网格单元以及左边和上边的相邻网格单元的幸福感贡献为 $h[up][i]+h[left][i]$；而当前网格单元本身的幸福感取决于该位置是否分配人员，以及分配的人员是内向的还是外向的，如果是内向的，那么幸福感为 $120$，如果是外向的，那么幸福感为 $40$，否则幸福感为 $0$；然后，如果当前网格单元分配了人员，那么我们递归调用时需要更新 $ic$ 或 $ec$。累计这些幸福感，取最大值作为函数的返回值。

与方法一类似，我们也可以使用记忆化搜索的方法，避免重复计算。

时间复杂度 $O(3^{n+1} \times m \times n \times ic \times ec)$，空间复杂度 $O(3^n \times m \times n \times ic \times ec)$。其中 $ic$ 和 $ec$ 分别表示内向的人和外向的人的个数。

Python3

class Solution:
    def getMaxGridHappiness(
        self, m: int, n: int, introvertsCount: int, extrovertsCount: int
    ) -> int:
        @cache
        def dfs(pos: int, pre: int, ic: int, ec: int) -> int:
            if pos == m * n or (ic == 0 and ec == 0):
                return 0
            ans = 0
            up = pre // p
            left = 0 if pos % n == 0 else pre % 3
            for i in range(3):
                if (i == 1 and ic == 0) or (i == 2 and ec == 0):
                    continue
                cur = pre % p * 3 + i
                a = h[up][i] + h[left][i]
                b = dfs(pos + 1, cur, ic - (i == 1), ec - (i == 2))
                c = 0
                if i == 1:
                    c = 120
                elif i == 2:
                    c = 40
                ans = max(ans, a + b + c)
            return ans

        p = pow(3, n - 1)
        h = [[0, 0, 0], [0, -60, -10], [0, -10, 40]]
        return dfs(0, 0, introvertsCount, extrovertsCount)

Java

class Solution {
    private int m;
    private int n;
    private int p;
    private final int[][] h = {{0, 0, 0}, {0, -60, -10}, {0, -10, 40}};
    private Integer[][][][] memo;

    public int getMaxGridHappiness(int m, int n, int introvertsCount, int extrovertsCount) {
        this.m = m;
        this.n = n;
        p = (int) Math.pow(3, n - 1);
        memo = new Integer[m * n][p * 3][introvertsCount + 1][extrovertsCount + 1];
        return dfs(0, 0, introvertsCount, extrovertsCount);
    }

    private int dfs(int pos, int pre, int ic, int ec) {
        if (pos == m * n || (ic == 0 && ec == 0)) {
            return 0;
        }
        if (memo[pos][pre][ic][ec] != null) {
            return memo[pos][pre][ic][ec];
        }
        int ans = 0;
        int up = pre / p;
        int left = pos % n == 0 ? 0 : pre % 3;
        for (int i = 0; i < 3; ++i) {
            if (i == 1 && (ic == 0) || (i == 2 && ec == 0)) {
                continue;
            }
            int cur = pre % p * 3 + i;
            int a = h[up][i] + h[left][i];
            int b = dfs(pos + 1, cur, ic - (i == 1 ? 1 : 0), ec - (i == 2 ? 1 : 0));
            int c = i == 1 ? 120 : (i == 2 ? 40 : 0);
            ans = Math.max(ans, a + b + c);
        }
        return memo[pos][pre][ic][ec] = ans;
    }
}

C++

class Solution {
public:
    int getMaxGridHappiness(int m, int n, int introvertsCount, int extrovertsCount) {
        int h[3][3] = {{0, 0, 0}, {0, -60, -10}, {0, -10, 40}};
        int p = pow(3, n - 1);
        int memo[m * n][p * 3][introvertsCount + 1][extrovertsCount + 1];
        memset(memo, -1, sizeof(memo));
        function<int(int, int, int, int)> dfs = [&](int pos, int pre, int ic, int ec) {
            if (pos == m * n || (ic == 0 && ec == 0)) {
                return 0;
            }
            if (memo[pos][pre][ic][ec] != -1) {
                return memo[pos][pre][ic][ec];
            }
            int ans = 0;
            int up = pre / p;
            int left = pos % n == 0 ? 0 : pre % 3;
            for (int i = 0; i < 3; ++i) {
                if ((i == 1 && ic == 0) || (i == 2 && ec == 0)) {
                    continue;
                }
                int cur = pre % p * 3 + i;
                int a = h[up][i] + h[left][i];
                int b = dfs(pos + 1, cur, ic - (i == 1), ec - (i == 2));
                int c = i == 1 ? 120 : (i == 2 ? 40 : 0);
                ans = max(ans, a + b + c);
            }
            return memo[pos][pre][ic][ec] = ans;
        };
        return dfs(0, 0, introvertsCount, extrovertsCount);
    }
};

Go

func getMaxGridHappiness(m int, n int, introvertsCount int, extrovertsCount int) int {
	p := int(math.Pow(3, float64(n-1)))
	h := [3][3]int{{0, 0, 0}, {0, -60, -10}, {0, -10, 40}}
	memo := make([][][][]int, m*n)
	for i := range memo {
		memo[i] = make([][][]int, p*3)
		for j := range memo[i] {
			memo[i][j] = make([][]int, introvertsCount+1)
			for k := range memo[i][j] {
				memo[i][j][k] = make([]int, extrovertsCount+1)
				for l := range memo[i][j][k] {
					memo[i][j][k][l] = -1
				}
			}
		}
	}
	var dfs func(int, int, int, int) int
	dfs = func(pos, pre, ic, ec int) int {
		if pos == m*n || (ic == 0 && ec == 0) {
			return 0
		}
		if memo[pos][pre][ic][ec] != -1 {
			return memo[pos][pre][ic][ec]
		}
		ans := 0
		up := pre / p
		left := pre % 3
		if pos%n == 0 {
			left = 0
		}
		for i := 0; i < 3; i++ {
			if (i == 1 && ic == 0) || (i == 2 && ec == 0) {
				continue
			}
			cur := pre%p*3 + i
			nic, nec := ic, ec
			c := 0
			if i == 1 {
				nic--
				c = 120
			} else if i == 2 {
				nec--
				c = 40
			}
			a := h[up][i] + h[left][i]
			b := dfs(pos+1, cur, nic, nec)
			ans = max(ans, a+b+c)
		}
		memo[pos][pre][ic][ec] = ans
		return ans
	}
	return dfs(0, 0, introvertsCount, extrovertsCount)
}

TypeScript

function getMaxGridHappiness(
    m: number,
    n: number,
    introvertsCount: number,
    extrovertsCount: number,
): number {
    const p = 3 ** (n - 1);
    const h: number[][] = [
        [0, 0, 0],
        [0, -60, -10],
        [0, -10, 40],
    ];
    const memo: number[][][][] = Array(m * n)
        .fill(0)
        .map(() =>
            Array(p * 3)
                .fill(0)
                .map(() =>
                    Array(introvertsCount + 1)
                        .fill(0)
                        .map(() => Array(extrovertsCount + 1).fill(-1)),
                ),
        );
    const dfs = (pos: number, pre: number, ic: number, ec: number): number => {
        if (pos === m * n || (ic === 0 && ec === 0)) {
            return 0;
        }
        if (memo[pos][pre][ic][ec] !== -1) {
            return memo[pos][pre][ic][ec];
        }
        let ans = 0;
        const up = Math.floor(pre / p);
        const left = pos % n == 0 ? 0 : pre % 3;
        for (let i = 0; i < 3; ++i) {
            if ((i === 1 && ic === 0) || (i === 2 && ec === 0)) {
                continue;
            }
            const cur = (pre % p) * 3 + i;
            const a = h[up][i] + h[left][i];
            const nic = i === 1 ? ic - 1 : ic;
            const nec = i === 2 ? ec - 1 : ec;
            const b = dfs(pos + 1, cur, nic, nec);
            const c = i === 1 ? 120 : i === 2 ? 40 : 0;
            ans = Math.max(ans, a + b + c);
        }
        return (memo[pos][pre][ic][ec] = ans);
    };
    return dfs(0, 0, introvertsCount, extrovertsCount);
}