Skip to content

Latest commit

 

History

History
231 lines (182 loc) · 6.39 KB

README.md

File metadata and controls

231 lines (182 loc) · 6.39 KB
Raw
comments difficulty edit_url rating source tags
true
中等
1521
第 210 场周赛 Q2
图

1615. 最大网络秩

English Version

题目描述

n 座城市和一些连接这些城市的道路 roads 共同组成一个基础设施网络。每个 roads[i] = [ai, bi] 都表示在城市 ai 和 bi 之间有一条双向道路。

两座不同城市构成的 城市对 的 网络秩 定义为：与这两座城市 直接 相连的道路总数。如果存在一条道路直接连接这两座城市，则这条道路只计算 一次 。

整个基础设施网络的 最大网络秩 是所有不同城市对中的 最大网络秩 。

给你整数 n 和数组 roads，返回整个基础设施网络的 最大网络秩 。

 

示例 1：

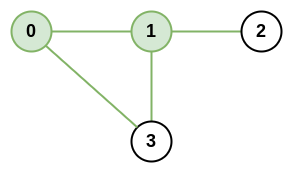
输入：n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
输出：4
解释：城市 0 和 1 的网络秩是 4，因为共有 4 条道路与城市 0 或 1 相连。位于 0 和 1 之间的道路只计算一次。

示例 2：

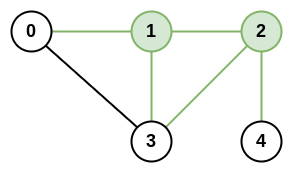
输入：n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
输出：5
解释：共有 5 条道路与城市 1 或 2 相连。

示例 3：

输入：n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
输出：5
解释：2 和 5 的网络秩为 5，注意并非所有的城市都需要连接起来。

 

提示：

  • 2 <= n <= 100
  • 0 <= roads.length <= n * (n - 1) / 2
  • roads[i].length == 2
  • 0 <= ai, bi <= n-1
  • ai != bi
  • 每对城市之间 最多只有一条 道路相连

解法

方法一：计数

我们可以用一维数组 $cnt$ 记录每个城市的度，用二维数组 $g$ 记录每对城市之间是否有道路相连，如果城市 $a$ 和城市 $b$ 之间有道路相连，则 $g[a][b] = g[b][a] = 1$，否则 $g[a][b] = g[b][a] = 0$。

接下来，我们枚举每对城市 $(a, b)$，其中 $a \lt b$，计算它们的网络秩，即 $cnt[a] + cnt[b] - g[a][b]$，取其中的最大值即为答案。

时间复杂度 $O(n^2)$，空间复杂度 $O(n^2)$。其中 $n$ 是城市的数量。

Python3

class Solution:
    def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:
        g = defaultdict(set)
        for a, b in roads:
            g[a].add(b)
            g[b].add(a)
        ans = 0
        for a in range(n):
            for b in range(a + 1, n):
                if (t := len(g[a]) + len(g[b]) - (a in g[b])) > ans:
                    ans = t
        return ans

Java

class Solution {
    public int maximalNetworkRank(int n, int[][] roads) {
        int[][] g = new int[n][n];
        int[] cnt = new int[n];
        for (var r : roads) {
            int a = r[0], b = r[1];
            g[a][b] = 1;
            g[b][a] = 1;
            ++cnt[a];
            ++cnt[b];
        }
        int ans = 0;
        for (int a = 0; a < n; ++a) {
            for (int b = a + 1; b < n; ++b) {
                ans = Math.max(ans, cnt[a] + cnt[b] - g[a][b]);
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int maximalNetworkRank(int n, vector<vector<int>>& roads) {
        int cnt[n];
        int g[n][n];
        memset(cnt, 0, sizeof(cnt));
        memset(g, 0, sizeof(g));
        for (auto& r : roads) {
            int a = r[0], b = r[1];
            g[a][b] = g[b][a] = 1;
            ++cnt[a];
            ++cnt[b];
        }
        int ans = 0;
        for (int a = 0; a < n; ++a) {
            for (int b = a + 1; b < n; ++b) {
                ans = max(ans, cnt[a] + cnt[b] - g[a][b]);
            }
        }
        return ans;
    }
};

Go

func maximalNetworkRank(n int, roads [][]int) (ans int) {
	g := make([][]int, n)
	cnt := make([]int, n)
	for i := range g {
		g[i] = make([]int, n)
	}
	for _, r := range roads {
		a, b := r[0], r[1]
		g[a][b], g[b][a] = 1, 1
		cnt[a]++
		cnt[b]++
	}
	for a := 0; a < n; a++ {
		for b := a + 1; b < n; b++ {
			ans = max(ans, cnt[a]+cnt[b]-g[a][b])
		}
	}
	return
}

TypeScript

function maximalNetworkRank(n: number, roads: number[][]): number {
    const g: number[][] = Array.from(new Array(n), () => new Array(n).fill(0));
    const cnt: number[] = new Array(n).fill(0);
    for (const [a, b] of roads) {
        g[a][b] = 1;
        g[b][a] = 1;
        ++cnt[a];
        ++cnt[b];
    }
    let ans = 0;
    for (let a = 0; a < n; ++a) {
        for (let b = a + 1; b < n; ++b) {
            ans = Math.max(ans, cnt[a] + cnt[b] - g[a][b]);
        }
    }
    return ans;
}

方法二

Python3

class Solution:
    def maximalNetworkRank(self, n: int, roads: List[List[int]]) -> int:
        g = [[0] * n for _ in range(n)]
        cnt = [0] * n
        for a, b in roads:
            g[a][b] = g[b][a] = 1
            cnt[a] += 1
            cnt[b] += 1
        return max(cnt[a] + cnt[b] - g[a][b] for a in range(n) for b in range(a + 1, n))