Skip to content

Latest commit

 

History

History
384 lines (320 loc) · 10.5 KB

README.md

File metadata and controls

384 lines (320 loc) · 10.5 KB
Raw
comments difficulty edit_url rating source tags
true
中等
1633
第 191 场周赛 Q3
深度优先搜索
广度优先搜索
图

1466. 重新规划路线

English Version

题目描述

n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

 

示例 1：

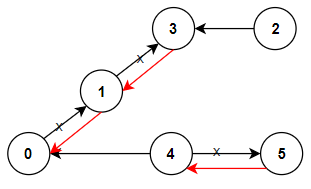
输入：n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
输出：3
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 2：

输入：n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
输出：2
解释：更改以红色显示的路线的方向，使每个城市都可以到达城市 0 。

示例 3：

输入：n = 3, connections = [[1,0],[2,0]]
输出：0

 

提示：

  • 2 <= n <= 5 * 10^4
  • connections.length == n-1
  • connections[i].length == 2
  • 0 <= connections[i][0], connections[i][1] <= n-1
  • connections[i][0] != connections[i][1]

解法

方法一：DFS

题目给定的路线图中有 $n$ 个节点和 $n-1$ 条边，如果我们忽略边的方向，那么这 $n$ 个节点构成了一棵树。而题目需要我们改变某些边的方向，使得每个节点都能到达节点 $0$。

我们不妨考虑从节点 $0$ 出发，到达其他所有节点。方向与题目描述相反，意味着我们在构建图的时候，对于有向边 $[a, b]$，我们应该视为有向边 $[b, a]$。也即是说，如果要从 $a$ 到 $b$，我们需要变更一次方向；如果要从 $b$ 到 $a$，则不需要变更方向。

接下来，我们只需要从节点 $0$ 出发，搜索其他所有节点，过程中，如果遇到需要变更方向的边，则累加一次变更方向的次数。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是题目中节点的数量。

Python3

class Solution:
    def minReorder(self, n: int, connections: List[List[int]]) -> int:
        def dfs(a: int, fa: int) -> int:
            return sum(c + dfs(b, a) for b, c in g[a] if b != fa)

        g = [[] for _ in range(n)]
        for a, b in connections:
            g[a].append((b, 1))
            g[b].append((a, 0))
        return dfs(0, -1)

Java

class Solution {
    private List<int[]>[] g;

    public int minReorder(int n, int[][] connections) {
        g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : connections) {
            int a = e[0], b = e[1];
            g[a].add(new int[] {b, 1});
            g[b].add(new int[] {a, 0});
        }
        return dfs(0, -1);
    }

    private int dfs(int a, int fa) {
        int ans = 0;
        for (var e : g[a]) {
            int b = e[0], c = e[1];
            if (b != fa) {
                ans += c + dfs(b, a);
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int minReorder(int n, vector<vector<int>>& connections) {
        vector<pair<int, int>> g[n];
        for (auto& e : connections) {
            int a = e[0], b = e[1];
            g[a].emplace_back(b, 1);
            g[b].emplace_back(a, 0);
        }
        function<int(int, int)> dfs = [&](int a, int fa) {
            int ans = 0;
            for (auto& [b, c] : g[a]) {
                if (b != fa) {
                    ans += c + dfs(b, a);
                }
            }
            return ans;
        };
        return dfs(0, -1);
    }
};

Go

func minReorder(n int, connections [][]int) int {
	g := make([][][2]int, n)
	for _, e := range connections {
		a, b := e[0], e[1]
		g[a] = append(g[a], [2]int{b, 1})
		g[b] = append(g[b], [2]int{a, 0})
	}
	var dfs func(int, int) int
	dfs = func(a, fa int) (ans int) {
		for _, e := range g[a] {
			if b, c := e[0], e[1]; b != fa {
				ans += c + dfs(b, a)
			}
		}
		return
	}
	return dfs(0, -1)
}

TypeScript

function minReorder(n: number, connections: number[][]): number {
    const g: [number, number][][] = Array.from({ length: n }, () => []);
    for (const [a, b] of connections) {
        g[a].push([b, 1]);
        g[b].push([a, 0]);
    }
    const dfs = (a: number, fa: number): number => {
        let ans = 0;
        for (const [b, c] of g[a]) {
            if (b !== fa) {
                ans += c + dfs(b, a);
            }
        }
        return ans;
    };
    return dfs(0, -1);
}

Rust

impl Solution {
    pub fn min_reorder(n: i32, connections: Vec<Vec<i32>>) -> i32 {
        let mut g: Vec<Vec<(i32, i32)>> = vec![vec![]; n as usize];
        for e in connections.iter() {
            let a = e[0] as usize;
            let b = e[1] as usize;
            g[a].push((b as i32, 1));
            g[b].push((a as i32, 0));
        }
        fn dfs(a: usize, fa: i32, g: &Vec<Vec<(i32, i32)>>) -> i32 {
            let mut ans = 0;
            for &(b, c) in g[a].iter() {
                if b != fa {
                    ans += c + dfs(b as usize, a as i32, g);
                }
            }
            ans
        }
        dfs(0, -1, &g)
    }
}

方法二：BFS

我们可以使用广度优先搜索的方法，从节点 $0$ 出发，搜索其他所有节点，过程中，如果遇到需要变更方向的边，则累加一次变更方向的次数。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 是题目中节点的数量。

Python3

class Solution:
    def minReorder(self, n: int, connections: List[List[int]]) -> int:
        g = [[] for _ in range(n)]
        for a, b in connections:
            g[a].append((b, 1))
            g[b].append((a, 0))
        q = deque([0])
        vis = {0}
        ans = 0
        while q:
            a = q.popleft()
            for b, c in g[a]:
                if b not in vis:
                    vis.add(b)
                    q.append(b)
                    ans += c
        return ans
class Solution {
    public int minReorder(int n, int[][] connections) {
        List<int[]>[] g = new List[n];
        Arrays.setAll(g, k -> new ArrayList<>());
        for (var e : connections) {
            int a = e[0], b = e[1];
            g[a].add(new int[] {b, 1});
            g[b].add(new int[] {a, 0});
        }
        Deque<Integer> q = new ArrayDeque<>();
        q.offer(0);
        boolean[] vis = new boolean[n];
        vis[0] = true;
        int ans = 0;
        while (!q.isEmpty()) {
            int a = q.poll();
            for (var e : g[a]) {
                int b = e[0], c = e[1];
                if (!vis[b]) {
                    vis[b] = true;
                    q.offer(b);
                    ans += c;
                }
            }
        }
        return ans;
    }
}
class Solution {
public:
    int minReorder(int n, vector<vector<int>>& connections) {
        vector<pair<int, int>> g[n];
        for (auto& e : connections) {
            int a = e[0], b = e[1];
            g[a].emplace_back(b, 1);
            g[b].emplace_back(a, 0);
        }
        queue<int> q{{0}};
        vector<bool> vis(n);
        vis[0] = true;
        int ans = 0;
        while (q.size()) {
            int a = q.front();
            q.pop();
            for (auto& [b, c] : g[a]) {
                if (!vis[b]) {
                    vis[b] = true;
                    q.push(b);
                    ans += c;
                }
            }
        }
        return ans;
    }
};
func minReorder(n int, connections [][]int) (ans int) {
	g := make([][][2]int, n)
	for _, e := range connections {
		a, b := e[0], e[1]
		g[a] = append(g[a], [2]int{b, 1})
		g[b] = append(g[b], [2]int{a, 0})
	}
	q := []int{0}
	vis := make([]bool, n)
	vis[0] = true
	for len(q) > 0 {
		a := q[0]
		q = q[1:]
		for _, e := range g[a] {
			b, c := e[0], e[1]
			if !vis[b] {
				vis[b] = true
				q = append(q, b)
				ans += c
			}
		}
	}
	return
}
function minReorder(n: number, connections: number[][]): number {
    const g: [number, number][][] = Array.from({ length: n }, () => []);
    for (const [a, b] of connections) {
        g[a].push([b, 1]);
        g[b].push([a, 0]);
    }

    const q: number[] = [0];
    const vis = new Set<number>();
    vis.add(0);

    let ans = 0;
    while (q.length) {
        const a = q.pop()!;
        for (const [b, c] of g[a]) {
            if (!vis.has(b)) {
                vis.add(b);
                q.push(b);
                ans += c;
            }
        }
    }
    return ans;
}