Skip to content

Latest commit

 

History

History
269 lines (217 loc) · 7.59 KB

README.md

File metadata and controls

269 lines (217 loc) · 7.59 KB
Raw
comments difficulty edit_url rating source tags
true
困难
1885
第 172 场周赛 Q4
贪心
数组
动态规划

1326. 灌溉花园的最少水龙头数目

English Version

题目描述

在 x 轴上有一个一维的花园。花园长度为 n，从点 0 开始，到点 n 结束。

花园里总共有 n + 1 个水龙头，分别位于 [0, 1, ..., n] 。

给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ，其中 ranges[i] （下标从 0 开始）表示：如果打开点 i 处的水龙头，可以灌溉的区域为 [i -  ranges[i], i + ranges[i]] 。

请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方，请你返回 -1 。

 

示例 1：

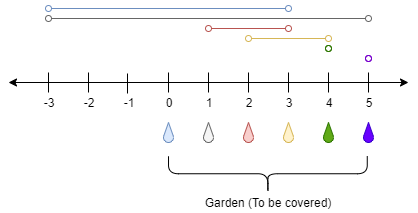
输入：n = 5, ranges = [3,4,1,1,0,0]
输出：1
解释：
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。

示例 2：

输入：n = 3, ranges = [0,0,0,0]
输出：-1
解释：即使打开所有水龙头，你也无法灌溉整个花园。

 

提示：

  • 1 <= n <= 104
  • ranges.length == n + 1
  • 0 <= ranges[i] <= 100

解法

方法一：贪心

我们注意到，对于所有能覆盖某个左端点的水龙头，选择能覆盖最远右端点的那个水龙头是最优的。

因此，我们可以先预处理数组 $ranges$，对于第 $i$ 个水龙头，它能覆盖的左端点 $l = \max(0, i - ranges[i])$，右端点 $r = i + ranges[i]$，我们算出所有能覆盖左端点 $l$ 的水龙头中，右端点最大的那个位置，记录在数组 $last[i]$ 中。

然后我们定义以下三个变量，其中：

  • 变量 $ans$ 表示最终答案，即最少水龙头数目；
  • 变量 $mx$ 表示当前能覆盖的最远右端点；
  • 变量 $pre$ 表示上一个水龙头覆盖的最远右端点。

我们在 $[0,...n-1]$ 的范围内遍历所有位置，对于当前位置 $i$，我们用 $last[i]$ 更新 $mx$，即 $mx = \max(mx, last[i])$。

  • 如果 $mx \leq i$，说明无法覆盖下一个位置，返回 $-1$。
  • 如果 $pre = i$，说明需要使用一个新的子区间，因此我们将 $ans$ 加 $1$，并且更新 $pre = mx$。

遍历结束后，返回 $ans$ 即可。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。其中 $n$ 为花园的长度。

相似题目：

Python3

class Solution:
    def minTaps(self, n: int, ranges: List[int]) -> int:
        last = [0] * (n + 1)
        for i, x in enumerate(ranges):
            l, r = max(0, i - x), i + x
            last[l] = max(last[l], r)

        ans = mx = pre = 0
        for i in range(n):
            mx = max(mx, last[i])
            if mx <= i:
                return -1
            if pre == i:
                ans += 1
                pre = mx
        return ans

Java

class Solution {
    public int minTaps(int n, int[] ranges) {
        int[] last = new int[n + 1];
        for (int i = 0; i < n + 1; ++i) {
            int l = Math.max(0, i - ranges[i]), r = i + ranges[i];
            last[l] = Math.max(last[l], r);
        }
        int ans = 0, mx = 0, pre = 0;
        for (int i = 0; i < n; ++i) {
            mx = Math.max(mx, last[i]);
            if (mx <= i) {
                return -1;
            }
            if (pre == i) {
                ++ans;
                pre = mx;
            }
        }
        return ans;
    }
}

C++

class Solution {
public:
    int minTaps(int n, vector<int>& ranges) {
        vector<int> last(n + 1);
        for (int i = 0; i < n + 1; ++i) {
            int l = max(0, i - ranges[i]), r = i + ranges[i];
            last[l] = max(last[l], r);
        }
        int ans = 0, mx = 0, pre = 0;
        for (int i = 0; i < n; ++i) {
            mx = max(mx, last[i]);
            if (mx <= i) {
                return -1;
            }
            if (pre == i) {
                ++ans;
                pre = mx;
            }
        }
        return ans;
    }
};

Go

func minTaps(n int, ranges []int) (ans int) {
	last := make([]int, n+1)
	for i, x := range ranges {
		l, r := max(0, i-x), i+x
		last[l] = max(last[l], r)
	}
	var pre, mx int
	for i, j := range last[:n] {
		mx = max(mx, j)
		if mx <= i {
			return -1
		}
		if pre == i {
			ans++
			pre = mx
		}
	}
	return
}

TypeScript

function minTaps(n: number, ranges: number[]): number {
    const last = new Array(n + 1).fill(0);
    for (let i = 0; i < n + 1; ++i) {
        const l = Math.max(0, i - ranges[i]);
        const r = i + ranges[i];
        last[l] = Math.max(last[l], r);
    }
    let ans = 0;
    let mx = 0;
    let pre = 0;
    for (let i = 0; i < n; ++i) {
        mx = Math.max(mx, last[i]);
        if (mx <= i) {
            return -1;
        }
        if (pre == i) {
            ++ans;
            pre = mx;
        }
    }
    return ans;
}

Rust

impl Solution {
    #[allow(dead_code)]
    pub fn min_taps(n: i32, ranges: Vec<i32>) -> i32 {
        let mut last = vec![0; (n + 1) as usize];
        let mut ans = 0;
        let mut mx = 0;
        let mut pre = 0;

        // Initialize the last vector
        for (i, &r) in ranges.iter().enumerate() {
            if (i as i32) - r >= 0 {
                last[((i as i32) - r) as usize] =
                    std::cmp::max(last[((i as i32) - r) as usize], (i as i32) + r);
            } else {
                last[0] = std::cmp::max(last[0], (i as i32) + r);
            }
        }

        for i in 0..n as usize {
            mx = std::cmp::max(mx, last[i]);
            if mx <= (i as i32) {
                return -1;
            }
            if pre == (i as i32) {
                ans += 1;
                pre = mx;
            }
        }

        ans
    }
}