Skip to content

Latest commit

 

History

History
598 lines (535 loc) · 15.9 KB

README_EN.md

File metadata and controls

598 lines (535 loc) · 15.9 KB
Raw
comments difficulty edit_url tags
true
Medium
Tree
Depth-First Search
Breadth-First Search
Binary Tree

655. Print Binary Tree

中文文档

Description

Given the root of a binary tree, construct a 0-indexed m x n string matrix res that represents a formatted layout of the tree. The formatted layout matrix should be constructed using the following rules:

  • The height of the tree is height and the number of rows m should be equal to height + 1.
  • The number of columns n should be equal to 2height+1 - 1.
  • Place the root node in the middle of the top row (more formally, at location res[0][(n-1)/2]).
  • For each node that has been placed in the matrix at position res[r][c], place its left child at res[r+1][c-2height-r-1] and its right child at res[r+1][c+2height-r-1].
  • Continue this process until all the nodes in the tree have been placed.
  • Any empty cells should contain the empty string "".

Return the constructed matrix res.

 

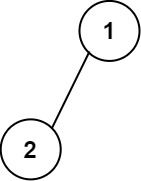
Example 1:

Input: root = [1,2]
Output: 
[["","1",""],
 ["2","",""]]

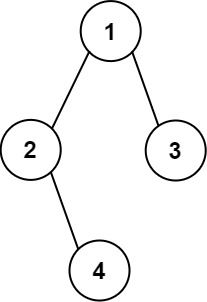
Example 2:

Input: root = [1,2,3,null,4]
Output: 
[["","","","1","","",""],
 ["","2","","","","3",""],
 ["","","4","","","",""]]

 

Constraints:

  • The number of nodes in the tree is in the range [1, 210].
  • -99 <= Node.val <= 99
  • The depth of the tree will be in the range [1, 10].

Solutions

Solution 1

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def printTree(self, root: Optional[TreeNode]) -> List[List[str]]:
        def height(root):
            if root is None:
                return -1
            return 1 + max(height(root.left), height(root.right))

        def dfs(root, r, c):
            if root is None:
                return
            ans[r][c] = str(root.val)
            dfs(root.left, r + 1, c - 2 ** (h - r - 1))
            dfs(root.right, r + 1, c + 2 ** (h - r - 1))

        h = height(root)
        m, n = h + 1, 2 ** (h + 1) - 1
        ans = [[""] * n for _ in range(m)]
        dfs(root, 0, (n - 1) // 2)
        return ans

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<String>> printTree(TreeNode root) {
        int h = height(root);
        int m = h + 1, n = (1 << (h + 1)) - 1;
        String[][] res = new String[m][n];
        for (int i = 0; i < m; ++i) {
            Arrays.fill(res[i], "");
        }
        dfs(root, res, h, 0, (n - 1) / 2);
        List<List<String>> ans = new ArrayList<>();
        for (String[] t : res) {
            ans.add(Arrays.asList(t));
        }
        return ans;
    }

    private void dfs(TreeNode root, String[][] res, int h, int r, int c) {
        if (root == null) {
            return;
        }
        res[r][c] = String.valueOf(root.val);
        dfs(root.left, res, h, r + 1, c - (1 << (h - r - 1)));
        dfs(root.right, res, h, r + 1, c + (1 << (h - r - 1)));
    }

    private int height(TreeNode root) {
        if (root == null) {
            return -1;
        }
        return 1 + Math.max(height(root.left), height(root.right));
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<string>> printTree(TreeNode* root) {
        int h = height(root);
        int m = h + 1, n = (1 << (h + 1)) - 1;
        vector<vector<string>> ans(m, vector<string>(n, ""));
        dfs(root, ans, h, 0, (n - 1) / 2);
        return ans;
    }

    void dfs(TreeNode* root, vector<vector<string>>& ans, int h, int r, int c) {
        if (!root) return;
        ans[r][c] = to_string(root->val);
        dfs(root->left, ans, h, r + 1, c - pow(2, h - r - 1));
        dfs(root->right, ans, h, r + 1, c + pow(2, h - r - 1));
    }

    int height(TreeNode* root) {
        if (!root) return -1;
        return 1 + max(height(root->left), height(root->right));
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func printTree(root *TreeNode) [][]string {
	var height func(root *TreeNode) int
	height = func(root *TreeNode) int {
		if root == nil {
			return -1
		}
		return 1 + max(height(root.Left), height(root.Right))
	}
	h := height(root)
	m, n := h+1, (1<<(h+1))-1
	ans := make([][]string, m)
	for i := range ans {
		ans[i] = make([]string, n)
		for j := range ans[i] {
			ans[i][j] = ""
		}
	}
	var dfs func(root *TreeNode, r, c int)
	dfs = func(root *TreeNode, r, c int) {
		if root == nil {
			return
		}
		ans[r][c] = strconv.Itoa(root.Val)
		dfs(root.Left, r+1, c-int(math.Pow(float64(2), float64(h-r-1))))
		dfs(root.Right, r+1, c+int(math.Pow(float64(2), float64(h-r-1))))
	}

	dfs(root, 0, (n-1)/2)
	return ans
}

TypeScript

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function printTree(root: TreeNode | null): string[][] {
    const getHeight = (root: TreeNode | null, h: number) => {
        if (root == null) {
            return h - 1;
        }
        return Math.max(getHeight(root.left, h + 1), getHeight(root.right, h + 1));
    };

    const height = getHeight(root, 0);
    const m = height + 1;
    const n = 2 ** (height + 1) - 1;
    const res: string[][] = Array.from({ length: m }, () => new Array(n).fill(''));
    const dfs = (root: TreeNode | null, i: number, j: number) => {
        if (root === null) {
            return;
        }
        const { val, left, right } = root;
        res[i][j] = val + '';
        dfs(left, i + 1, j - 2 ** (height - i - 1));
        dfs(right, i + 1, j + 2 ** (height - i - 1));
    };
    dfs(root, 0, (n - 1) >>> 1);
    return res;
}

Rust

// Definition for a binary tree node.
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
//   pub val: i32,
//   pub left: Option<Rc<RefCell<TreeNode>>>,
//   pub right: Option<Rc<RefCell<TreeNode>>>,
// }
//
// impl TreeNode {
//   #[inline]
//   pub fn new(val: i32) -> Self {
//     TreeNode {
//       val,
//       left: None,
//       right: None
//     }
//   }
// }
use std::cell::RefCell;
use std::rc::Rc;
impl Solution {
    fn get_height(root: &Option<Rc<RefCell<TreeNode>>>, h: u32) -> u32 {
        if let Some(node) = root {
            let node = node.borrow();
            return Self::get_height(&node.left, h + 1).max(Self::get_height(&node.right, h + 1));
        }
        h - 1
    }

    fn dfs(
        root: &Option<Rc<RefCell<TreeNode>>>,
        i: usize,
        j: usize,
        res: &mut Vec<Vec<String>>,
        height: u32,
    ) {
        if root.is_none() {
            return;
        }
        let node = root.as_ref().unwrap().borrow();
        res[i][j] = node.val.to_string();
        Self::dfs(
            &node.left,
            i + 1,
            j - (2usize).pow(height - (i as u32) - 1),
            res,
            height,
        );
        Self::dfs(
            &node.right,
            i + 1,
            j + (2usize).pow(height - (i as u32) - 1),
            res,
            height,
        );
    }

    pub fn print_tree(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<Vec<String>> {
        let height = Self::get_height(&root, 0);
        let m = (height + 1) as usize;
        let n = (2usize).pow(height + 1) - 1;
        let mut res = vec![vec![String::new(); n]; m];
        Self::dfs(&root, 0, (n - 1) >> 1, &mut res, height);
        res
    }
}

Solution 2

Python3

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def printTree(self, root: Optional[TreeNode]) -> List[List[str]]:
        def height(root):
            q = deque([root])
            h = -1
            while q:
                h += 1
                for _ in range(len(q)):
                    root = q.popleft()
                    if root.left:
                        q.append(root.left)
                    if root.right:
                        q.append(root.right)
            return h

        h = height(root)
        m, n = h + 1, 2 ** (h + 1) - 1
        ans = [[""] * n for _ in range(m)]
        q = deque([(root, 0, (n - 1) // 2)])
        while q:
            node, r, c = q.popleft()
            ans[r][c] = str(node.val)
            if node.left:
                q.append((node.left, r + 1, c - 2 ** (h - r - 1)))
            if node.right:
                q.append((node.right, r + 1, c + 2 ** (h - r - 1)))
        return ans

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<String>> printTree(TreeNode root) {
        int h = height(root);
        int m = h + 1, n = (1 << (h + 1)) - 1;
        String[][] res = new String[m][n];
        for (int i = 0; i < m; ++i) {
            Arrays.fill(res[i], "");
        }
        Deque<Tuple> q = new ArrayDeque<>();
        q.offer(new Tuple(root, 0, (n - 1) / 2));
        while (!q.isEmpty()) {
            Tuple p = q.pollFirst();
            root = p.node;
            int r = p.r, c = p.c;
            res[r][c] = String.valueOf(root.val);
            if (root.left != null) {
                q.offer(new Tuple(root.left, r + 1, c - (1 << (h - r - 1))));
            }
            if (root.right != null) {
                q.offer(new Tuple(root.right, r + 1, c + (1 << (h - r - 1))));
            }
        }
        List<List<String>> ans = new ArrayList<>();
        for (String[] t : res) {
            ans.add(Arrays.asList(t));
        }
        return ans;
    }

    private int height(TreeNode root) {
        Deque<TreeNode> q = new ArrayDeque<>();
        q.offer(root);
        int h = -1;
        while (!q.isEmpty()) {
            ++h;
            for (int n = q.size(); n > 0; --n) {
                root = q.pollFirst();
                if (root.left != null) {
                    q.offer(root.left);
                }
                if (root.right != null) {
                    q.offer(root.right);
                }
            }
        }
        return h;
    }
}

class Tuple {
    TreeNode node;
    int r;
    int c;

    public Tuple(TreeNode node, int r, int c) {
        this.node = node;
        this.r = r;
        this.c = c;
    }
}

C++

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<string>> printTree(TreeNode* root) {
        int h = height(root);
        int m = h + 1, n = (1 << (h + 1)) - 1;
        vector<vector<string>> ans(m, vector<string>(n, ""));
        queue<tuple<TreeNode*, int, int>> q;
        q.push({root, 0, (n - 1) / 2});
        while (!q.empty()) {
            auto p = q.front();
            q.pop();
            root = get<0>(p);
            int r = get<1>(p), c = get<2>(p);
            ans[r][c] = to_string(root->val);
            if (root->left) q.push({root->left, r + 1, c - pow(2, h - r - 1)});
            if (root->right) q.push({root->right, r + 1, c + pow(2, h - r - 1)});
        }
        return ans;
    }

    int height(TreeNode* root) {
        int h = -1;
        queue<TreeNode*> q{{root}};
        while (!q.empty()) {
            ++h;
            for (int n = q.size(); n; --n) {
                root = q.front();
                q.pop();
                if (root->left) q.push(root->left);
                if (root->right) q.push(root->right);
            }
        }
        return h;
    }
};

Go

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func printTree(root *TreeNode) [][]string {
	h := height(root)
	m, n := h+1, (1<<(h+1))-1
	ans := make([][]string, m)
	for i := range ans {
		ans[i] = make([]string, n)
		for j := range ans[i] {
			ans[i][j] = ""
		}
	}
	q := []tuple{tuple{root, 0, (n - 1) / 2}}
	for len(q) > 0 {
		p := q[0]
		q = q[1:]
		root := p.node
		r, c := p.r, p.c
		ans[r][c] = strconv.Itoa(root.Val)
		if root.Left != nil {
			q = append(q, tuple{root.Left, r + 1, c - int(math.Pow(float64(2), float64(h-r-1)))})
		}
		if root.Right != nil {
			q = append(q, tuple{root.Right, r + 1, c + int(math.Pow(float64(2), float64(h-r-1)))})
		}
	}
	return ans
}

func height(root *TreeNode) int {
	h := -1
	q := []*TreeNode{root}
	for len(q) > 0 {
		h++
		for n := len(q); n > 0; n-- {
			root := q[0]
			q = q[1:]
			if root.Left != nil {
				q = append(q, root.Left)
			}
			if root.Right != nil {
				q = append(q, root.Right)
			}
		}
	}
	return h
}

type tuple struct {
	node *TreeNode
	r    int
	c    int
}